Home » Subject » Graph Theory
Importance: Medium ✭✭
Author(s): Bentz, Cedric
Subject: Graph Theory
Keywords: approximation algorithms
planar graph
polynomial algorithm
Recomm. for undergrads: no
Posted by: jcmeyer
on: April 18th, 2010
Conjecture   Is the approximation ratio for the Maximum Edge Disjoint Paths (MaxEDP) or the Maximum Integer Multiflow problem (MaxIMF) bounded by a constant in $ k $-outerplanar graphs or tree-width graphs?

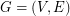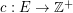Assume a flow graph $ G = (V, E) $ with $ n $ vertices and $ m $ edges (Flow network). Each edge has a capacity function $ c: E \rightarrow \mathbb{Z}^+ $. The graph contains a list 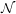$ \mathcal{N} $ of terminal vertices called sources (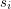$ s_i $) and sinks (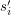$ s_i' $). Each pair (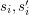$ s_i, s_i' $) defines a net or commodity.

A Multiflow is a way of routing commodities from their sources to the respective sinks while ensuring that the flow of each commodity is conserved at each non-terminal vertex and that the sum of the flows of all commodities through an edge does not exceed the capacity of the edge.

The Maximum Integer Multiflow problem (MaxIMF) seeks to maximize the number of flow units routed between the nets in the graph. The Maximum Edge Disjoint Paths (MaxEDP) problem seeks to find the maximum number of disjoint paths between the sources and sinks. When the capacities for all edges are set to one, MaxIMF simplifies into the MaxEDP problem.

Is the approximation ratio (Approximation and integrality gap) for MaxEDP or MaxIMF bounded by a constant in $ k $-outerplanar graphs (Outerplanar graphs) or tree-width graphs?

Bibliography

C. Bentz, “Disjoint paths in sparse graphs,” Discrete Appl. Math., vol. 157, no. 17, pp. 3558–3568, 2009


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options