Home » Subject » Graph Theory
Importance: Medium ✭✭
Author(s): Bentz, Cedric
Subject: Graph Theory
Keywords: planar graph
polynomial algorithm
Recomm. for undergrads: no
Posted by: jcmeyer
on: April 18th, 2010
Conjecture   It has been shown that a $ k $-outerplanar embedding for which $ k $ is minimal can be found in polynomial time. Does a similar result hold for $ k $-edge-outerplanar graphs?

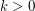A $ k $-outerplanar graph [Baker] with $ k > 0 $ is a planar graph having an embedding with at most $ k $ layers of vertices such that after removing iteratively the vertices (and their adjacent edges) lying on the outer face $ k $ times, we obtain the empty graph.

A $ k $-edge-outerplanar graph [Bentz] is defined to be a planar graph having an embedding with at most $ k $ layers of edges such that after removing iteratively the edges lying on the outer face $ k $ times, we obtain a graph with no edge. All $ k $-edge-outerplanar graphs are $ k $-outerplanar graphs.

Given a planar graph, Bienstock and Monma have shown that a $ k $-outerplanar embedding for which $ k $ is minimal can be found in polynomial time. Does a similar result hold for $ k $-edge-outerplanar graphs?

Bibliography

C. Bentz, “Disjoint paths in sparse graphs,” Discrete Appl. Math., vol. 157, no. 17, pp. 3558–3568, 2009

D. Bienstock and C. L. Monma, “On the complexity of embedding planar graphs to minimize certain distance measures,” Algorithmica, vol. 5, no. 1–4, pp. 93–109, 1990

B. S. Baker, “Approximation algorithms for np-complete problems on planar graphs,” J. ACM, vol. 41, no. 1, pp. 153–180, 1994


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options