 login/create account
login/create account
Eschen, Elaine M.
The stubborn list partition problem ★★
Author(s): Cameron; Eschen; Hoang; Sritharan
Problem Does there exist a polynomial time algorithm which takes as input a graph  and for every vertex
and for every vertex 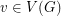 a subset
a subset 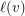 of
of 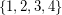 , and decides if there exists a partition of
, and decides if there exists a partition of 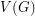 into
into 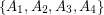 so that
so that 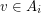 only if
only if 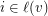 and so that
and so that 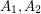 are independent,
are independent, 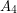 is a clique, and there are no edges between
is a clique, and there are no edges between 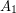 and
and  ?
?
 and for every vertex
and for every vertex 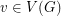 a subset
a subset 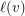 of
of 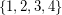 , and decides if there exists a partition of
, and decides if there exists a partition of 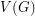 into
into 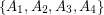 so that
so that 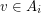 only if
only if 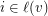 and so that
and so that 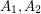 are independent,
are independent, 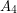 is a clique, and there are no edges between
is a clique, and there are no edges between 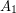 and
and  ?
? Keywords: list partition; polynomial algorithm

 Drupal
Drupal CSI of Charles University
CSI of Charles University