 login/create account
login/create account
Approximation ratio for k-outerplanar graphs
 -outerplanar graphs or tree-width graphs?
-outerplanar graphs or tree-width graphs? Assume a flow graph 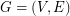 with
with  vertices and
vertices and  edges (Flow network). Each edge has a capacity function
edges (Flow network). Each edge has a capacity function 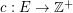 . The graph contains a list
. The graph contains a list 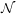 of terminal vertices called sources (
of terminal vertices called sources (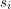 ) and sinks (
) and sinks (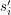 ). Each pair (
). Each pair (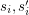 ) defines a net or commodity.
) defines a net or commodity.
A Multiflow is a way of routing commodities from their sources to the respective sinks while ensuring that the flow of each commodity is conserved at each non-terminal vertex and that the sum of the flows of all commodities through an edge does not exceed the capacity of the edge.
The Maximum Integer Multiflow problem (MaxIMF) seeks to maximize the number of flow units routed between the nets in the graph. The Maximum Edge Disjoint Paths (MaxEDP) problem seeks to find the maximum number of disjoint paths between the sources and sinks. When the capacities for all edges are set to one, MaxIMF simplifies into the MaxEDP problem.
Is the approximation ratio (Approximation and integrality gap) for MaxEDP or MaxIMF bounded by a constant in  -outerplanar graphs (Outerplanar graphs) or tree-width graphs?
-outerplanar graphs (Outerplanar graphs) or tree-width graphs?
Bibliography
C. Bentz, “Disjoint paths in sparse graphs,” Discrete Appl. Math., vol. 157, no. 17, pp. 3558–3568, 2009
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University