 login/create account
login/create account
What is the largest graph of positive curvature?
Definition: For a graph  embedded in the sphere, the combinatorial curvature of a vertex
embedded in the sphere, the combinatorial curvature of a vertex  is defined to be
is defined to be 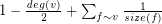 (here the summation is over all faces
(here the summation is over all faces  incident with
incident with  ).
).
Let  be a graph embedded in the sphere, and consider the polygonal surface formed by treating each face of size
be a graph embedded in the sphere, and consider the polygonal surface formed by treating each face of size  as a regular
as a regular  -gon of side length
-gon of side length 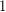 . The gaussian curvature at a vertex
. The gaussian curvature at a vertex  is defined to be
is defined to be 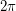 minus the sum of the angles incident with
minus the sum of the angles incident with  . So, our vertex
. So, our vertex  has positive curvature if the sum of the incident angles is less than
has positive curvature if the sum of the incident angles is less than 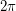 . In fact, the combinatorial curvature at
. In fact, the combinatorial curvature at  is exactly
is exactly 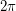 times the gaussian curvature, so these quantities will always have the same sign.
times the gaussian curvature, so these quantities will always have the same sign.
Let us call a convex polyhedron regular-faced if each face is a regular polygon. Based on the previous discussion, we know that every convex regular-faced polyhedron gives us a graph with everywhere positive combinatorial curvature. Indeed, we may view planar graphs with everywhere positive curvature as a kind of generalization of these polyhedra. The polyhedra in this class have been studied and classified. The Platonic solids and Archimedean solids are all convex and regular faced, and there are two infinite families: prisms and antiprisms. In addition to this, there are 92 other exceptional ones, known as Johnson Solids.
Euler's formula tells us that the sum of the combinatorial curvatures over all of the vertices is equal to 2. Indeed, the combinatorial curvature is exactly what we get when we assign 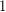 to each vertex and face,
to each vertex and face, 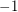 to each edge, and then "discharge" evenly onto the vertices. So, if we wish to construct large planar graphs where every vertex has positive curvature, we will need to make the curvature arbitrarily small. This can be achieved with prisms and antiprisms, but apart from these two families, all other graphs with everywhere positive curvature have a bounded number of vertices. Improving upon [DM], Zhang [Z] has shown this upper bound to be at most 580. The great rhombicosidodecahedron has 120 vertices and everywhere positive curvature (this is the largest regular-faced convex polyhedron which is not a prism or antiprism). Reti, Bitay, and Kosztolanyi [RBK] have improved upon this lower bound by constructing a graph with everywhere positive curvature and 138 vertices. These are the best bounds I (M. DeVos) know of.
to each edge, and then "discharge" evenly onto the vertices. So, if we wish to construct large planar graphs where every vertex has positive curvature, we will need to make the curvature arbitrarily small. This can be achieved with prisms and antiprisms, but apart from these two families, all other graphs with everywhere positive curvature have a bounded number of vertices. Improving upon [DM], Zhang [Z] has shown this upper bound to be at most 580. The great rhombicosidodecahedron has 120 vertices and everywhere positive curvature (this is the largest regular-faced convex polyhedron which is not a prism or antiprism). Reti, Bitay, and Kosztolanyi [RBK] have improved upon this lower bound by constructing a graph with everywhere positive curvature and 138 vertices. These are the best bounds I (M. DeVos) know of.
Bibliography
[DM] M. DeVos and B. Mohar, An analogue of the Descarte-Euler formula for infinite graphs and Higuchi's conjecture preprint.
[H] Y. Higuchi, Combinatorial curvature for planar graph, J. Graph Theory, Vol 38 (2001), no. 4, 220-229. MathSciNet
[RBK] T. Reti, E. Bitay, and Zs. Kosztolanyi, On the polyhedral graphs with positive combinatorial curvature, Acta Polytechnica Hungarica Vol. 2, No. 2 (2005) 19-37.
[Z] L. Zhang, A result on combinatorial curvature for embedded graphs on a surface, Discrete Math (2007) in press
* indicates original appearance(s) of problem.
project underway
This is an active project for an honours student at the University of Auckland. We'd be interested in hearing from anyone else working on the problem: contact j.sneddon@auckland.ac.nz

 Drupal
Drupal CSI of Charles University
CSI of Charles University
new 'largest' PCC graph
We have a new largest PCC graph with 208 vertices, improving the lower bound.
It will be published soon in the New Zealand Journal of Mathematics. "New graphs with thinly spread positive combinatorial curvature." j.sneddon@auckland.ac.nz