 login/create account
login/create account
Drawing disconnected graphs on surfaces
Conjecture Let  be the disjoint union of the graphs
be the disjoint union of the graphs 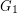 and
and 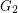 and let
and let 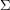 be a surface. Is it true that every optimal drawing of
be a surface. Is it true that every optimal drawing of  on
on 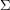 has the property that
has the property that 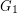 and
and 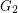 are disjoint?
are disjoint?
 be the disjoint union of the graphs
be the disjoint union of the graphs 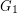 and
and 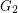 and let
and let 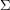 be a surface. Is it true that every optimal drawing of
be a surface. Is it true that every optimal drawing of  on
on 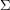 has the property that
has the property that 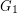 and
and 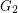 are disjoint?
are disjoint? We insist on the usual restrictions for drawings (as in The Crossing Number of the Complete Graph).
Although both crossing numbers and embeddings of graphs on general surfaces are rich and well-studied subjects, their common generalization - drawing graphs on general surfaces has received very little attention. The question highlighted here appears to be quite basic in nature, but due to the combined difficulties of crossings and general surfaces, it may be quite difficult to resolve.
This conjecture is trivially true when 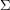 is the plane, and DeVos, Mohar, and Samal have proved that it also holds when
is the plane, and DeVos, Mohar, and Samal have proved that it also holds when 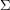 is the projective plane. It is open for all other surfaces to the best of my (M. DeVos) knowledge.
is the projective plane. It is open for all other surfaces to the best of my (M. DeVos) knowledge.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Drawing disconnected graphs on surfaces : any reference ?
Hello,
You don't mention reference in this problem, though it is said that some work has been made. Would it be possible to know how the projective plane has been shown to verify this conjecture ?
Thanks in advance for any piece of information.
Laurent Beaudou