 login/create account
login/create account
The Crossing Number of the Complete Graph
The crossing number 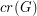 of
of  is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of  in the plane.
in the plane.
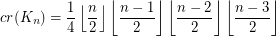
(This discussion appears as [M].)
A drawing of a graph  in the plane has the vertices represented by distinct points and the edges represented by polygonal lines joining their endpoints such that:
in the plane has the vertices represented by distinct points and the edges represented by polygonal lines joining their endpoints such that:
- \item no edge contains a vertex other than its endpoints, \item no two adjacent edges share a point other than their common endpoint, \item two nonadjacent edges share at most one point at which they cross transversally, and \item no three edges cross at the same point.
The conjectured value for the crossing number of  is known to be an upper bound. This is shown by exhibiting a drawing with that number of crossings. If
is known to be an upper bound. This is shown by exhibiting a drawing with that number of crossings. If 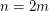 , place
, place  vertices regularly spaced along two circles of radii 1 and 2, respectively. Two vertices on the inner circle are connected by a straight line; two vertices on the outer circle are connected by a polygonal line outside the circle. A vertex on the inner circle is connected to one on the outer circle with a polygonal line segment of minimum possible positive winding angle around the cylinder. A simple count shows that the number of crossings in such a drawing achieves the conjectured minimum. For
vertices regularly spaced along two circles of radii 1 and 2, respectively. Two vertices on the inner circle are connected by a straight line; two vertices on the outer circle are connected by a polygonal line outside the circle. A vertex on the inner circle is connected to one on the outer circle with a polygonal line segment of minimum possible positive winding angle around the cylinder. A simple count shows that the number of crossings in such a drawing achieves the conjectured minimum. For 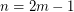 we delete one vertex from the drawing described and achieve the conjectured minimum.
we delete one vertex from the drawing described and achieve the conjectured minimum.
The conjecture is known to be true for  at most 10 [G]. If the conjecture is true for
at most 10 [G]. If the conjecture is true for 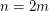 , then it is also true for
, then it is also true for 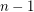 . This follows from an argument counting the number of crossings in drawings of all
. This follows from an argument counting the number of crossings in drawings of all 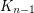 's contained in an optimal drawing of
's contained in an optimal drawing of 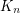 .
.
It would also be interesting to prove that the conjectured upper bound is asymptotically correct, that is, that 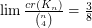 .
.
The best known lower bound is due to Kleitman [K], who showed that this limit is at least 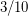 .
.
Bibliography
[G] R. Guy, The decline and fall of Zarankiewicz's theorem, in Proof Techniques in Graph Theory (F. Harary Ed.), Academic Press, New York (1969) 63-69.
[K] D. Kleitman, The crossing number of 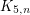 , J. Combin. Theory 9 (1970) 315-323.
, J. Combin. Theory 9 (1970) 315-323.
[M] B. Mohar, Problem of the Month
* indicates original appearance(s) of problem.
This is not the best known bound.
The same article below, that proves that 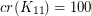 and
and 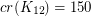 , states that
, states that 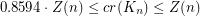 .
.
true upto n=12
The conjecture was recently verified for n=11 and 12 (The Crossing Number of 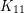 Is 100 by Shengjun Pan and R. Bruce Richter).
Is 100 by Shengjun Pan and R. Bruce Richter).

 Drupal
Drupal CSI of Charles University
CSI of Charles University
On lower bound.
It has been shown that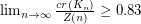 , where
, where 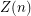 is the conjectured value. For the proof, see de Klerk, E.; Maharry, J.; Pasechnik, D. V.; Richter, R. B.; Salazar, G. Improved bounds for the crossing numbers of
is the conjectured value. For the proof, see de Klerk, E.; Maharry, J.; Pasechnik, D. V.; Richter, R. B.; Salazar, G. Improved bounds for the crossing numbers of 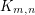 and
and 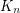 . (2007).
. (2007).