 login/create account
login/create account
packing
Inequality of the means ★★★
Author(s):
Question Is is possible to pack 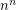 rectangular
rectangular  -dimensional boxes each of which has side lengths
-dimensional boxes each of which has side lengths 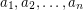 inside an
inside an  -dimensional cube with side length
-dimensional cube with side length 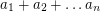 ?
?
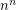 rectangular
rectangular  -dimensional boxes each of which has side lengths
-dimensional boxes each of which has side lengths 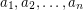 inside an
inside an  -dimensional cube with side length
-dimensional cube with side length 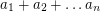 ?
? Keywords: arithmetic mean; geometric mean; Inequality; packing
Ding's tau_r vs. tau conjecture ★★★
Author(s): Ding
Conjecture Let 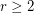 be an integer and let
be an integer and let  be a minor minimal clutter with
be a minor minimal clutter with  . Then either
. Then either  has a
has a 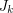 minor for some
minor for some 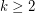 or
or  has Lehman's property.
has Lehman's property.
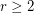 be an integer and let
be an integer and let  be a minor minimal clutter with
be a minor minimal clutter with  . Then either
. Then either  has a
has a 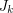 minor for some
minor for some 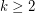 or
or  has Lehman's property.
has Lehman's property. Keywords: clutter; covering; MFMC property; packing
Woodall's Conjecture ★★★
Author(s): Woodall
Conjecture If  is a directed graph with smallest directed cut of size
is a directed graph with smallest directed cut of size  , then
, then  has
has  disjoint dijoins.
disjoint dijoins.
 is a directed graph with smallest directed cut of size
is a directed graph with smallest directed cut of size  , then
, then  has
has  disjoint dijoins.
disjoint dijoins. Ryser's conjecture ★★★
Author(s): Ryser
Conjecture Let  be an
be an  -uniform
-uniform  -partite hypergraph. If
-partite hypergraph. If  is the maximum number of pairwise disjoint edges in
is the maximum number of pairwise disjoint edges in  , and
, and  is the size of the smallest set of vertices which meets every edge, then
is the size of the smallest set of vertices which meets every edge, then 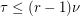 .
.
 be an
be an  -uniform
-uniform  -partite hypergraph. If
-partite hypergraph. If  is the maximum number of pairwise disjoint edges in
is the maximum number of pairwise disjoint edges in  , and
, and  is the size of the smallest set of vertices which meets every edge, then
is the size of the smallest set of vertices which meets every edge, then 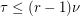 .
. Keywords: hypergraph; matching; packing
Packing T-joins ★★
Author(s): DeVos
Conjecture There exists a fixed constant  (probably
(probably 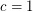 suffices) so that every graft with minimum
suffices) so that every graft with minimum  -cut size at least
-cut size at least  contains a
contains a  -join packing of size at least
-join packing of size at least 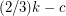 .
.
 (probably
(probably 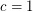 suffices) so that every graft with minimum
suffices) so that every graft with minimum  -cut size at least
-cut size at least  contains a
contains a  -join packing of size at least
-join packing of size at least 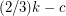 .
. 
 Drupal
Drupal CSI of Charles University
CSI of Charles University