 login/create account
login/create account
Inequality
Inequality for square summable complex series ★★
Author(s): Retkes
Conjecture For all 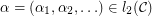 the following inequality holds
the following inequality holds 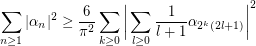
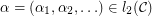 the following inequality holds
the following inequality holds 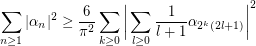
Keywords: Inequality
Inequality of the means ★★★
Author(s):
Question Is is possible to pack 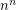 rectangular
rectangular  -dimensional boxes each of which has side lengths
-dimensional boxes each of which has side lengths 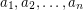 inside an
inside an  -dimensional cube with side length
-dimensional cube with side length 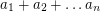 ?
?
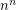 rectangular
rectangular  -dimensional boxes each of which has side lengths
-dimensional boxes each of which has side lengths 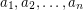 inside an
inside an  -dimensional cube with side length
-dimensional cube with side length 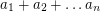 ?
? Keywords: arithmetic mean; geometric mean; Inequality; packing
Sums of independent random variables with unbounded variance ★★
Author(s): Feige
Conjecture If 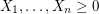 are independent random variables with
are independent random variables with ![$ \mathbb{E}[X_i] \leq \mu $](/files/tex/e0268221532981debea25e9446c8ee6f112e1881.png) , then
, then ![$$\mathrm{Pr} \left( \sum X_i - \mathbb{E} \left[ \sum X_i \right ] < \delta \mu \right) \geq \min \left ( (1 + \delta)^{-1} \delta, e^{-1} \right).$$](/files/tex/03dc1130142ee6fefcc33888e2fb6137211bf327.png)
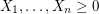 are independent random variables with
are independent random variables with ![$ \mathbb{E}[X_i] \leq \mu $](/files/tex/e0268221532981debea25e9446c8ee6f112e1881.png) , then
, then ![$$\mathrm{Pr} \left( \sum X_i - \mathbb{E} \left[ \sum X_i \right ] < \delta \mu \right) \geq \min \left ( (1 + \delta)^{-1} \delta, e^{-1} \right).$$](/files/tex/03dc1130142ee6fefcc33888e2fb6137211bf327.png)
Keywords: Inequality; Probability Theory; randomness in TCS

 Drupal
Drupal CSI of Charles University
CSI of Charles University