 login/create account
login/create account
Ding, Guoli
Ding's tau_r vs. tau conjecture ★★★
Author(s): Ding
Conjecture Let 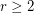 be an integer and let
be an integer and let  be a minor minimal clutter with
be a minor minimal clutter with  . Then either
. Then either  has a
has a 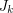 minor for some
minor for some 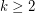 or
or  has Lehman's property.
has Lehman's property.
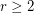 be an integer and let
be an integer and let  be a minor minimal clutter with
be a minor minimal clutter with  . Then either
. Then either  has a
has a 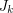 minor for some
minor for some 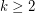 or
or  has Lehman's property.
has Lehman's property. Keywords: clutter; covering; MFMC property; packing
Bounded colorings for planar graphs ★★
Author(s): Alon; Ding; Oporowski; Vertigan
Question Does there exists a fixed function 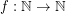 so that every planar graph of maximum degree
so that every planar graph of maximum degree  has a partition of its vertex set into at most three sets
has a partition of its vertex set into at most three sets 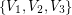 so that for
so that for 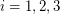 , every component of the graph induced by
, every component of the graph induced by 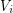 has size at most
has size at most 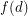 ?
?
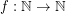 so that every planar graph of maximum degree
so that every planar graph of maximum degree  has a partition of its vertex set into at most three sets
has a partition of its vertex set into at most three sets 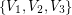 so that for
so that for 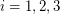 , every component of the graph induced by
, every component of the graph induced by 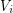 has size at most
has size at most 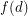 ?
? Keywords: coloring; partition; planar graph

 Drupal
Drupal CSI of Charles University
CSI of Charles University