 login/create account
login/create account
hypergraph
A generalization of Vizing's Theorem? ★★
Author(s): Rosenfeld
Conjecture Let  be a simple
be a simple  -uniform hypergraph, and assume that every set of
-uniform hypergraph, and assume that every set of 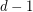 points is contained in at most
points is contained in at most  edges. Then there exists an
edges. Then there exists an 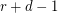 -edge-coloring so that any two edges which share
-edge-coloring so that any two edges which share 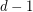 vertices have distinct colors.
vertices have distinct colors.
 be a simple
be a simple  -uniform hypergraph, and assume that every set of
-uniform hypergraph, and assume that every set of 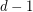 points is contained in at most
points is contained in at most  edges. Then there exists an
edges. Then there exists an 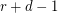 -edge-coloring so that any two edges which share
-edge-coloring so that any two edges which share 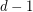 vertices have distinct colors.
vertices have distinct colors. Keywords: edge-coloring; hypergraph; Vizing
Ryser's conjecture ★★★
Author(s): Ryser
Conjecture Let  be an
be an  -uniform
-uniform  -partite hypergraph. If
-partite hypergraph. If  is the maximum number of pairwise disjoint edges in
is the maximum number of pairwise disjoint edges in  , and
, and  is the size of the smallest set of vertices which meets every edge, then
is the size of the smallest set of vertices which meets every edge, then 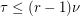 .
.
 be an
be an  -uniform
-uniform  -partite hypergraph. If
-partite hypergraph. If  is the maximum number of pairwise disjoint edges in
is the maximum number of pairwise disjoint edges in  , and
, and  is the size of the smallest set of vertices which meets every edge, then
is the size of the smallest set of vertices which meets every edge, then 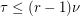 .
. Keywords: hypergraph; matching; packing

 Drupal
Drupal CSI of Charles University
CSI of Charles University