Home » Subject » Graph Theory » Coloring » Nowhere-zero flows

Antichains in the cycle continuous order

Importance: Medium ✭✭
Author(s): DeVos, Matt
Subject: Graph Theory
» Coloring
» » Nowhere-zero flows
Keywords: antichain
cycle
poset
Recomm. for undergrads: no
Prize: Bottle of wine (DeVos)
Posted by: mdevos
on: May 12th, 2007

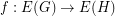If $ G $,$ H $ are graphs, a function $ f : E(G) \rightarrow E(H) $ is called cycle-continuous if the pre-image of every element of the (binary) cycle space of $ H $ is a member of the cycle space of $ G $.

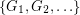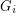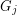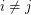Problem   Does there exist an infinite set of graphs $ \{G_1,G_2,\ldots \} $ so that there is no cycle continuous mapping between $ G_i $ and $ G_j $ whenever $ i \neq j $ ?

The definition of a cycle-continuous mapping is based on some work of Jaeger, and the most interesting question on this subject is undoubtedly Jaeger's Petersen coloring conjecture.

Let us define a relation on the set of all finite graphs with at least one edge by the rule 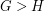$ G>H $ if there is a cycle-continuous mapping from $ G $ to $ H $. It is not difficult to verify that $ > $ is a quasi order (reflexive and transitive). In this order, every Eulerian graph dominates every other graph, and every graph with a cut edge is dominated by every other graph.

Let 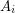$ A_i $ be the graph on two vertices with $ i $ parallel edges. Then $ A_3 < A_5 < A_7 < ... $ with all the inequalities strict, so this sequence is an infinite chain. Very little else seems to be known about this order. In particular, the problem highlighted above - does there exist an infinite antichain? remains open.

Bibliography



* indicates original appearance(s) of problem.
add new comment