 login/create account
login/create account
tension
5-local-tensions ★★
Author(s): DeVos
Conjecture There exists a fixed constant  (probably
(probably 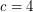 suffices) so that every embedded (loopless) graph with edge-width
suffices) so that every embedded (loopless) graph with edge-width 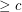 has a 5-local-tension.
has a 5-local-tension.
 (probably
(probably 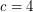 suffices) so that every embedded (loopless) graph with edge-width
suffices) so that every embedded (loopless) graph with edge-width 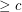 has a 5-local-tension.
has a 5-local-tension. A homomorphism problem for flows ★★
Author(s): DeVos
Conjecture Let 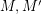 be abelian groups and let
be abelian groups and let 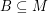 and
and 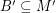 satisfy
satisfy 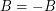 and
and 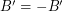 . If there is a homomorphism from
. If there is a homomorphism from 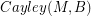 to
to 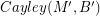 , then every graph with a B-flow has a B'-flow.
, then every graph with a B-flow has a B'-flow.
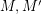 be abelian groups and let
be abelian groups and let 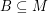 and
and 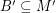 satisfy
satisfy 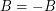 and
and 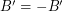 . If there is a homomorphism from
. If there is a homomorphism from 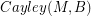 to
to 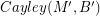 , then every graph with a B-flow has a B'-flow.
, then every graph with a B-flow has a B'-flow. Keywords: homomorphism; nowhere-zero flow; tension

 Drupal
Drupal CSI of Charles University
CSI of Charles University