Home » Subject » Number Theory » Combinatorial N.T.

Gao's theorem for nonabelian groups

Importance: Medium ✭✭
Author(s): DeVos, Matt
Subject: Number Theory
» Combinatorial Number Theory
Keywords: subsequence sum
zero sum
Recomm. for undergrads: no
Posted by: mdevos
on: May 23rd, 2007

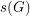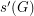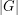For every finite multiplicative group $ G $, let $ s(G) $ ($ s'(G) $) denote the smallest integer $ m $ so that every sequence of $ m $ elements of $ G $ has a subsequence of length $ >0 $ (length $ |G| $) which has product equal to 1 in some order.

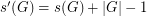Conjecture   $ s'(G) = s(G) + |G| - 1 $ for every finite group $ G $.

A beautiful theorem of Gao (previously conjectured by Caro) shows that the above property holds for all abelian groups. Rather surprisingly, almost all of the proof for the abelian case seems to work as well for the general case - only one rather innocent looking bit does not carry through. Next we explore this curiosity in detail, beginning with an easy observation.

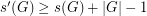Observation   $ s'(G) \ge s(G) + |G| - 1 $ for every (finite) group $ G $.

To see this, choose a sequence of length 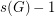$ s(G) - 1 $ of elements which has no nontrivial subsequence with product equal to 1 in any order. Now, append 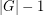$ |G| - 1 $ copies of 1 to this sequence. The new sequence has length 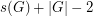$ s(G) + |G| - 2 $ and has no subsequence of length 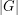$ |G| $ with product 1 in any order.

So, the hard part of Gao's theorem is to prove 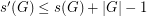$ s'(G) \le s(G) + |G| - 1 $, and we now have multiple proofs of this fact. One of the nicest arguments uses a theorem of Kempermann-Scherck, and can be split into the following two parts.

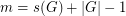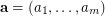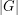Lemma   Let $ m = s(G) + |G| - 1 $ and let $ {\bf a} = (a_1,\ldots,a_m) $ be a sequence in an arbitrary finite multiplicative $ G $ with the added property that 1 is the most frequently occurring in $ {\bf a} $. Then there is a subsequence of $ {\bf a} $ of length $ |G| $ which has product equal to 1 in some order.
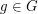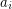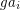Observation   If $ {\bf a} $ is a sequence of elements in the finite abelian group $ G $ and $ g \in G $, then replacing each element $ a_i $ of $ {\bf a} $ by $ ga_i $ has no effect on the products of length 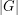$ |G| $ subsequences of $ {\bf a} $.

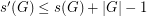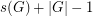The lemma and observation now combine easily to show $ s'(G) \le s(G) + |G| - 1 $ in abelian groups, since we may take any sequence $ {\bf a} $ of length $ s(G) + |G| - 1 $ and modify it by mutiplying each element by a fixed constant so that 1 is the most common element of $ {\bf a} $. The lemma shows that there is now a subsequence with product 1, and the observation shows that the corresponding subsequence has product 1 in the original. So, surprisingly, the Lemma - which includes all of the real difficutly - works just fine for general groups. The only place we required the assumption $ G $ is abelian is for the observation.

add new comment