 login/create account
login/create account
invertible
The permanent conjecture ★★
Author(s): Kahn
Conjecture If  is an invertible
is an invertible 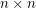 matrix, then there is an
matrix, then there is an 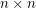 submatrix
submatrix  of
of ![$ [A A] $](/files/tex/d1e9d82c656535b507686183e640178057fae455.png) so that
so that 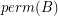 is nonzero.
is nonzero.
 is an invertible
is an invertible 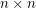 matrix, then there is an
matrix, then there is an 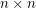 submatrix
submatrix  of
of ![$ [A A] $](/files/tex/d1e9d82c656535b507686183e640178057fae455.png) so that
so that 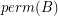 is nonzero.
is nonzero. Keywords: invertible; matrix; permanent
A nowhere-zero point in a linear mapping ★★★
Author(s): Jaeger
Conjecture If 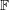 is a finite field with at least 4 elements and
is a finite field with at least 4 elements and  is an invertible
is an invertible 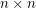 matrix with entries in
matrix with entries in 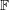 , then there are column vectors
, then there are column vectors 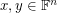 which have no coordinates equal to zero such that
which have no coordinates equal to zero such that 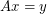 .
.
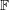 is a finite field with at least 4 elements and
is a finite field with at least 4 elements and  is an invertible
is an invertible 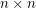 matrix with entries in
matrix with entries in 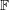 , then there are column vectors
, then there are column vectors 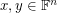 which have no coordinates equal to zero such that
which have no coordinates equal to zero such that 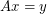 .
. Keywords: invertible; nowhere-zero flow

 Drupal
Drupal CSI of Charles University
CSI of Charles University