 login/create account
login/create account
Tarsi, Michael
Coloring the union of degenerate graphs ★★
Author(s): Tarsi
Conjecture The union of a 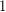 -degenerate graph (a forest) and a
-degenerate graph (a forest) and a  -degenerate graph is
-degenerate graph is  -colourable.
-colourable.
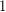 -degenerate graph (a forest) and a
-degenerate graph (a forest) and a  -degenerate graph is
-degenerate graph is  -colourable.
-colourable. Keywords:
Even vs. odd latin squares ★★★
A latin square is even if the product of the signs of all of the row and column permutations is 1 and is odd otherwise.
Conjecture For every positive even integer  , the number of even latin squares of order
, the number of even latin squares of order  and the number of odd latin squares of order
and the number of odd latin squares of order  are different.
are different.
 , the number of even latin squares of order
, the number of even latin squares of order  and the number of odd latin squares of order
and the number of odd latin squares of order  are different.
are different. Keywords: latin square
The additive basis conjecture ★★★
Author(s): Jaeger; Linial; Payan; Tarsi
Conjecture For every prime  , there is a constant
, there is a constant 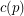 (possibly
(possibly 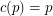 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 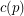 bases of the vector space
bases of the vector space 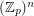 contains an additive basis.
contains an additive basis.
 , there is a constant
, there is a constant 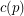 (possibly
(possibly 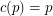 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 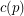 bases of the vector space
bases of the vector space 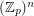 contains an additive basis.
contains an additive basis. Keywords: additive basis; matrix

 Drupal
Drupal CSI of Charles University
CSI of Charles University