 login/create account
login/create account
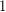 -degenerate graph (a forest) and a
-degenerate graph (a forest) and a  -degenerate graph is
-degenerate graph is  -colourable.
-colourable. A graph is  -degenerate if it can be reduced to
-degenerate if it can be reduced to 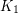 (the graph with a unique vertex) by repeatedly deleting vertices of degree at most
(the graph with a unique vertex) by repeatedly deleting vertices of degree at most  . A
. A 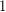 -degenerate graph
-degenerate graph 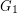 admits a proper
admits a proper  -colouring
-colouring 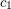 , and a
, and a  -degenerate graph
-degenerate graph 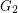 admits a proper
admits a proper  -colouring
-colouring 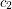 . Thus,
. Thus, 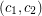 is a proper
is a proper  -colouring of
-colouring of 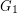 and
and 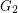 .
.
The conjecture is tigth because 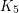 is the union of a
is the union of a 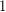 -degenerate graph and a
-degenerate graph and a  -degenerate graph.
-degenerate graph.
Based on a decompostion of the complete graph, Klein and Schönheim [KlSc93] generalised this conjecture to 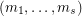 -composed graphs, which are unions of
-composed graphs, which are unions of  graphs
graphs 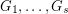 such that
such that 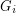 is
is 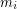 -degenerate,
-degenerate, 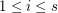 .
.
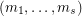 -composed graph is
-composed graph is 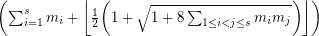 -colourable.
-colourable. Partial results towards this conjecture are obtained in [KlSc95].
Bibliography
*[K] R. Klein. On the colorability of { }-composed graphs. Discrete Math. 133 (1994), 181--190.
}-composed graphs. Discrete Math. 133 (1994), 181--190.
[KlSc93] R. Klein and J. Schönheim. Decomposition of {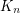 } into degenerate graphs. In Combinatorics and graph theory (Hefei, 1992), pages 141--155. World Sci. Publ., River Edge, NJ, 1993.
} into degenerate graphs. In Combinatorics and graph theory (Hefei, 1992), pages 141--155. World Sci. Publ., River Edge, NJ, 1993.
[KlSc95] R. Klein and J. Schönheim. On the colorability of graphs decomposable into degenerate graphs with specified degeneracy. Australas. J. Combin., 12:201--208, 1995.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University