 login/create account
login/create account
Even vs. odd latin squares
A latin square is even if the product of the signs of all of the row and column permutations is 1 and is odd otherwise.
 , the number of even latin squares of order
, the number of even latin squares of order  and the number of odd latin squares of order
and the number of odd latin squares of order  are different.
are different. For every positive integer  , let
, let 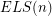 , (
, (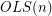 ) be the number of even (odd) latin squares of order
) be the number of even (odd) latin squares of order  .
.
The inspiration for this conjecture comes from an attempt by Alon and Tarsi to use their polynomial technique to show that the complete bipartite graph 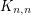 is
is  -edge-choosable (a famous conjecture of Dinitz asserts that this is always true). They show (in [AT]) that whenever
-edge-choosable (a famous conjecture of Dinitz asserts that this is always true). They show (in [AT]) that whenever 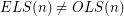 , the graph
, the graph 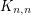 is
is  -edge-choosable. For odd integers
-edge-choosable. For odd integers 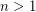 it is easy to see that
it is easy to see that 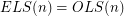 , since interchanging the first two rows has no effect on the signs of the rows, but flips the signs of all of the columns. For even
, since interchanging the first two rows has no effect on the signs of the rows, but flips the signs of all of the columns. For even  , Alon and Tarsi checked that
, Alon and Tarsi checked that 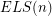 and
and 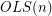 were different for
were different for 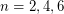 and conjectured that this pattern would continue. Although Dinitz' Conjecture has since been resolved, Alon and Tarsi's conjecture remains quite interesting. In particular, it has been shown by Huang and Rota [HR] that the truth of this conjecture would imply Rota's basis conjecture for even values of
and conjectured that this pattern would continue. Although Dinitz' Conjecture has since been resolved, Alon and Tarsi's conjecture remains quite interesting. In particular, it has been shown by Huang and Rota [HR] that the truth of this conjecture would imply Rota's basis conjecture for even values of  (see [O] for a nice proof of this).
(see [O] for a nice proof of this).
ELS() and OLS() appear in the The Encyclopedia of Integer Sequences as A114628 and A114629. The following chart shows the first few values. Although the data here is quite limited, 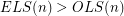 for every even
for every even  in the chart, and as far as we know, this might hold in general.
in the chart, and as far as we know, this might hold in general.
| n | ELS(n) | OLS(n) |
| 1 | 1 | 0 |
| 2 | 2 | 0 |
| 3 | 6 | 6 |
| 4 | 576 | 0 |
| 5 | 80640 | 80640 |
| 6 | 505958400 | 306892800 |
| 7 | 30739709952000 | 30739709952000 |
| 8 | 55019078005712486400 | 53756954453370470400 |
Drisko [D1] proved that whenever 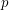 is prime,
is prime, 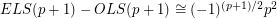 (mod
(mod 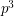 ), thus verifying the Alon-Tarsi conjecture for any even number which is one more than a prime. Shortly afterward, Zappa [Z] introduced a function
), thus verifying the Alon-Tarsi conjecture for any even number which is one more than a prime. Shortly afterward, Zappa [Z] introduced a function 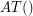 which compares the number of even and odd latin squares which have all diagonal entries equal to one, and proved some interesting identities concerning
which compares the number of even and odd latin squares which have all diagonal entries equal to one, and proved some interesting identities concerning  . By utilizing these identities, Drisko [D2] proved that
. By utilizing these identities, Drisko [D2] proved that 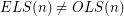 whenever
whenever  is of the form
is of the form 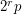 for a prime
for a prime 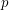 .
.
Bibliography
*[AT] N. Alon, M. Tarsi, Coloring and Orientations of Graphs. Combinatorica 12, 125-143, 1992 MathSciNet
[D1] A. Drisko, On the number of even and odd Latin squares of order 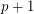 , Adv. Math. 128 (1997), no. 1, 20--35. MathSciNet
, Adv. Math. 128 (1997), no. 1, 20--35. MathSciNet
[D2] A. Drisko, Proof of the Alon-Tarsi conjecture for 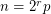 . Electron. J. Combin. 5 (1998) MathSciNet.
. Electron. J. Combin. 5 (1998) MathSciNet.
[HR] R. Huang and G-C Rota, On the relations of various conjectures on Latin squares and straightening coefficients. Discrete Math. 128 (1994), no. 1-3, 225--236. MathSciNet.
[O] S. Onn, A colorful determinantal identity, a conjecture of Rota, and Latin squares. Amer. Math. Monthly 104 (1997), no. 2, 156--159. MathSciNet.
[Z] P. Zappa, The Cayley determinant of the determinant tensor and the Alon-Tarsi conjecture. Adv. in Appl. Math. 19 (1997), no. 1, 31--44. MathSciNet.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University