 login/create account
login/create account
cubic
Exponentially many perfect matchings in cubic graphs ★★★
Conjecture There exists a fixed constant  so that every
so that every  -vertex cubic graph without a cut-edge has at least
-vertex cubic graph without a cut-edge has at least 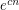 perfect matchings.
perfect matchings.
 so that every
so that every  -vertex cubic graph without a cut-edge has at least
-vertex cubic graph without a cut-edge has at least 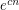 perfect matchings.
perfect matchings. Keywords: cubic; perfect matching
Bigger cycles in cubic graphs ★★
Author(s):
Problem Let  be a cyclically 4-edge-connected cubic graph and let
be a cyclically 4-edge-connected cubic graph and let  be a cycle of
be a cycle of  . Must there exist a cycle
. Must there exist a cycle 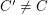 so that
so that 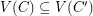 ?
?
 be a cyclically 4-edge-connected cubic graph and let
be a cyclically 4-edge-connected cubic graph and let  be a cycle of
be a cycle of  . Must there exist a cycle
. Must there exist a cycle 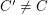 so that
so that 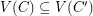 ?
? The intersection of two perfect matchings ★★
Conjecture Every bridgeless cubic graph has two perfect matchings 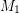 ,
, 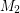 so that
so that 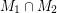 does not contain an odd edge-cut.
does not contain an odd edge-cut.
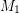 ,
, 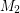 so that
so that 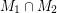 does not contain an odd edge-cut.
does not contain an odd edge-cut. Keywords: cubic; nowhere-zero flow; perfect matching
Barnette's Conjecture ★★★
Author(s): Barnette
Conjecture Every 3-connected cubic planar bipartite graph is Hamiltonian.
Keywords: bipartite; cubic; hamiltonian
Pentagon problem ★★★
Author(s): Nesetril
Question Let  be a 3-regular graph that contains no cycle of length shorter than
be a 3-regular graph that contains no cycle of length shorter than  . Is it true that for large enough~
. Is it true that for large enough~ there is a homomorphism
there is a homomorphism 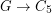 ?
?
 be a 3-regular graph that contains no cycle of length shorter than
be a 3-regular graph that contains no cycle of length shorter than  . Is it true that for large enough~
. Is it true that for large enough~ there is a homomorphism
there is a homomorphism 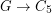 ?
? Keywords: cubic; homomorphism
The Berge-Fulkerson conjecture ★★★★
Conjecture If  is a bridgeless cubic graph, then there exist 6 perfect matchings
is a bridgeless cubic graph, then there exist 6 perfect matchings 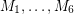 of
of  with the property that every edge of
with the property that every edge of  is contained in exactly two of
is contained in exactly two of 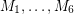 .
.
 is a bridgeless cubic graph, then there exist 6 perfect matchings
is a bridgeless cubic graph, then there exist 6 perfect matchings 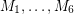 of
of  with the property that every edge of
with the property that every edge of  is contained in exactly two of
is contained in exactly two of 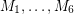 .
.
Keywords: cubic; perfect matching
5-flow conjecture ★★★★
Author(s): Tutte
Conjecture Every bridgeless graph has a nowhere-zero 5-flow.
Keywords: cubic; nowhere-zero flow

 Drupal
Drupal CSI of Charles University
CSI of Charles University