The Berge-Fulkerson conjecture

Importance: Outstanding ✭✭✭✭

Author(s):	Berge, Claude
	Fulkerson, Delbert R.

Subject:	Graph Theory
	» Basic Graph Theory
	» » Matchings

Keywords:	cubic
	perfect matching

Recomm. for undergrads: no

Posted	by:	mdevos
	on:	March 7th, 2007

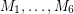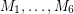Conjecture If $G$ is a bridgeless cubic graph, then there exist 6 perfect matchings $M_1,\ldots,M_6$ of $G$ with the property that every edge of $G$ is contained in exactly two of $M_1,\ldots,M_6$ .

This conjecture is due to Berge and Fulkerson, and appears first in [F] (see [S79b]).

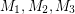If $G$ is 3-edge-colorable, then we may choose three perfect matchings $M_1,M_2,M_3$ so that every edge is in exactly one. Taking each of these twice gives us 6 perfect matchings with the properties described above. Thus, the above conjecture holds trivially for 3-edge-colorable graphs. There do exist bridgeless cubic graphs which are not 3-edge-colorable (for instance the Petersen graph), but the above conjecture asserts that every such graph is close to being 3-edge-colorable.

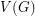Definition: An $r$ -graph is an $r$ -regular graph $G$ on an even number of vertices with the property that every edge-cut which separates $V(G)$ into two sets of odd cardinality has size at least $r$ .

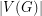Observe that a cubic graph is a 3-graph if and only if it has no bridge. If G is an $r$ -regular graph which has an $r$ -edge-coloring, then every color class is a perfect matching, so $|V(G)|$ must be even, and every color must appear in every edge-cut which separates 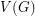$V(G)$ into two sets of odd size, so every edge-cut of this form must have size at least $r$ . Thus, every $r$ -edge-colorable $r$ -regular graph is an $r$ -graph. In a sense, we may view the $r$ -graphs as the $r$ -regular graphs which have the obvious necessary conditions to be $r$ -edge-colorable. Seymour [S79b] defined $r$ -graphs and offered the following generalization of the Berge-Fulkerson conjecture.

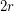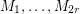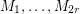Conjecture (The generalized Berge-Fulkerson conjecture (Seymour)) Let $G$ be an $r$ -graph. Then there exist $2r$ perfect matchings $M_1,\ldots,M_{2r}$ of $G$ with the property that every edge of $G$ is contained in exactly two of $M_1,\ldots,M_{2r}$ .

More generally, for a graph 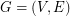$G=(V,E)$ , one may consider the vector space of real numbers indexed by 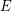$E$ . We associate every perfect matching 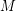$M$ with its characteristic vector. In this context, the Berge-Fulkerson conjecture asserts that for every 3-graph, the vector which is identically 1 may be written as a half-integer combination of perfect matchings. Edmonds matching polytope theorem [E] gives a complete characterization of what vectors in 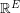${\mathbb R}^E$ which can be written as a nonnegative real combination of perfect matchings. A particular consequence of this theorem is that the vector which is identically 1 can be written as a nonnegative rational combination of perfect matchings if G is an $r$ -graph. 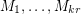It follows from this that for every $r$ -graph $G$ , there is a list of perfect matchings $M_1,\ldots,M_{kr}$ so that every edge is contained in exactly $k$ of them. Unfortunately, the particular $k$ depends on the graph. The following weak version of the Berge-Fulkerson conjecture asserts that this dependence is inessential.

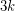Conjecture (the weak Berge-Fulkerson conjecture) There exists a positive integer $k$ with the following property. Every 3-graph $G$ has a list of $3k$ perfect matchings such that every edge of $G$ is contained in exactly $k$ of them.

There is a fascinating theorem of Lovasz [L] that characterizes which vectors in 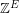${\mathbb Z}^E$ can be written as an integer combination of perfect matchings. However, very little is known about nonnegative integer combinations of perfect matchings. In particular, if the Berge-Fulkerson conjecture is true, then for every 3-graph 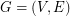$G=(V,E)$ , there is a list of 5 perfect matchings with union 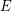$E$ (take any 5 of the 6 perfect matchings given by the conjecture). The following weakening of this (suggested by Berge) is still open.

Conjecture There exists a fixed integer $k$ such that the edge set of every 3-graph can be written as a union of $k$ perfect matchings.

Another consequence of the Berge-Fulkerson conjecture would be that every 3-graph has 3 perfect matchings with empty intersection (take any 3 of the 6 perfect matchings given by the conjecture). The following weakening of this (also suggested by Berge) is still open.

Conjecture There exists a fixed integer $k$ such that every 3-graph has a list of $k$ perfect matchings with empty intersection.

Bibliography

[E] J. Edmonds, Maximum matching and a polyhedron with 0,1-vertices, J. Res. Nat. Bur Stand B, Math & Math Phys. 69B (1965), 125-130.

[F] D.R. Fulkerson, Blocking and anti-blocking pairs of polyhedra, Math. Programming 1 (1971) 168-194. MathSciNet

[KKN] T. Kaiser, D. Kral, and S. Norine, Unions of perfect matchings in cubic graphs

[L] L. Lovasz, Matching structure and the matching lattice, J. Combin. Theory Ser. B 43 (1987), 187-222. MathSciNet

[R] R. Rizzi, Indecomposable r-graphs and some other counterexamples, J. Graph Theory 32 (1999), 1-15. MathSciNet

[S79a] P.D. Seymour, "Some unsolved problems on one-factorizations of graphs", Graph theory and Related Topics, J.A. Bondy and U.S.R. Murty (Editors), Academic, New York (1979), 367-368.

[S79b] P.D. Seymour, On multi-colourings of cubic graphs, and conjectures of Fulkerson and Tutte, Proc. London Math Soc. 38 (1979), 423-460. MathSciNet

* indicates original appearance(s) of problem.

add new comment

equivalent conjecture

On April 4th, 2011 Louis Esperet says:

It was recently proved by G Mazzuocolo (The Equivalence of Two Conjectures of Berge and Fulkerson, J. Graph Theory (2010) doi:10.1002/jgt.20545), that Berge-Fulkerson is indeed equivalent to the statement that for any 3-graph G, the edge-set of G can be covered by 5 perfect matchings. This might be worth mentioning it.

Covering with perfect matchings

On February 25th, 2009 Andrew King says:

It is not hard to show that you can cover the edges of a bridgeless cubic graph with 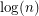$\log(n)$ perfect matchings. Is there some smaller-order function that suffices?

I believe this is best known

On February 25th, 2009 mdevos says:

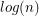The $log(n)$ bound you mention (a consequence of Edmond's perfect matching polytope theorem) is, to my knowledge, the best known lower bound.

Reference for log(n) bound

On October 16th, 2011 Emilio Brazil says:

I'm working with bridgeless cubic graphs and this bound is a good theoretical bound for my purposes. I'd like to know references for this 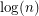$\log(n)$ bound.

log(n) bound

On November 23rd, 2011 Andrew King says:

The proof is basically the same as Lovász' proof that 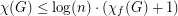$\chi(G) \leq \log(n)\cdot (\chi_f(G)+1)$ : It is well-known that the fractional chromatic number of a bridgeless cubic graph is 3. Therefore there is a probability distribution on the perfect matchings of $G$ such that given a random matching from this distribution, an edge $e$ is hit with probability 1/3.

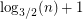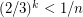Now let $k$ be $\log_{3/2}(n)+1$ and take $k$ perfect matchings from this distribution, and consider the probability that an edge $e$ is in none of them. This is $(2/3)^k < 1/n$ , so by the union bound, the probability that every edge is in one of the matchings is greater than 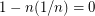$1- n(1/n) = 0$ . Therefore there is some choice of $k$ perfect matchings that cover the graph.

Best known upper bound

On November 22nd, 2011 Anonymous says:

I believe that the best known upper bound is given here http://arxiv.org/abs/1111.1871

Matchings and odd cuts

On March 2nd, 2009 Andrew King says:

I like thinking about this problem in terms of fractional colourings. A roughly equivalent proof (to the one you mentioned) is as follows. In a fractional 3-edge-colouring, every matching must be a perfect matching. The weights on the matchings, when divided by 3, give you a probability distribution. If you pick 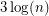$3 \log(n)$ matchings from this distribution, the union bound tells you that with positive probability you hit every edge. This method is powerful enough to prove that the fractional and integer chromatic numbers are always within a factor of 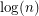$\log(n)$ of one another.

Here are two even weaker questions:

Is there some $k$ such that any bridgeless cubic graph contains $k$ perfect matchings whose intersection does not contain an odd cut?

Does every bridgeless cubic graph contain two perfect matchings that together hit no 5-cut 8 or 10 times?

I suspect both of these are open as well.

Sure

On March 4th, 2009 mdevos says:

Okay, sure, but the proof that there exists a fractional 3-edge-coloring is either a corollary of Edmond's Theorem or something essentially equivalent to it (such as the approach Seymour uses in his paper on r-graphs). In short, I agree that we are talking about essentially the same argument.

I believe that your first question is open. It is a well known conjecture (elsewhere on this site) that there should be 2 perfect matchings whose intersection does not contain an odd cut.

The second question has been resolved (using Edmond's theorem) by Kaiser, Kral, and Norine and I will add a link to the paper in the reference section.

proof of log(n)

On October 14th, 2011 Anonymous says:

Do you know a reference for a proof this log(n) boundary? I looked for it in text book but I don't have any clue.

Open Problem Garden