Home » The Berge-Fulkerson conjecture

log(n) bound

On November 23rd, 2011 Andrew King says:

The proof is basically the same as Lovász' proof that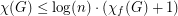 $ \chi(G) \leq \log(n)\cdot (\chi_f(G)+1) $: It is well-known that the fractional chromatic number of a bridgeless cubic graph is 3. Therefore there is a probability distribution on the perfect matchings of $ G $ such that given a random matching from this distribution, an edge $ e $ is hit with probability 1/3.

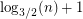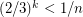Now let $ k $ be $ \log_{3/2}(n)+1 $ and take $ k $ perfect matchings from this distribution, and consider the probability that an edge $ e $ is in none of them. This is $ (2/3)^k < 1/n $, so by the union bound, the probability that every edge is in one of the matchings is greater than 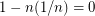$ 1- n(1/n) = 0 $. Therefore there is some choice of $ k $ perfect matchings that cover the graph.

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options