 login/create account
login/create account
Berge, Claude
Linial-Berge path partition duality ★★★
Conjecture The minimum  -norm of a path partition on a directed graph
-norm of a path partition on a directed graph  is no more than the maximal size of an induced
is no more than the maximal size of an induced  -colorable subgraph.
-colorable subgraph.
 -norm of a path partition on a directed graph
-norm of a path partition on a directed graph  is no more than the maximal size of an induced
is no more than the maximal size of an induced  -colorable subgraph.
-colorable subgraph. Keywords: coloring; directed path; partition
The Berge-Fulkerson conjecture ★★★★
Conjecture If  is a bridgeless cubic graph, then there exist 6 perfect matchings
is a bridgeless cubic graph, then there exist 6 perfect matchings 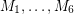 of
of  with the property that every edge of
with the property that every edge of  is contained in exactly two of
is contained in exactly two of 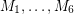 .
.
 is a bridgeless cubic graph, then there exist 6 perfect matchings
is a bridgeless cubic graph, then there exist 6 perfect matchings 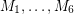 of
of  with the property that every edge of
with the property that every edge of  is contained in exactly two of
is contained in exactly two of 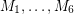 .
.
Keywords: cubic; perfect matching

 Drupal
Drupal CSI of Charles University
CSI of Charles University