 login/create account
login/create account
perfect matching
Exponentially many perfect matchings in cubic graphs ★★★
Conjecture There exists a fixed constant  so that every
so that every  -vertex cubic graph without a cut-edge has at least
-vertex cubic graph without a cut-edge has at least 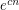 perfect matchings.
perfect matchings.
 so that every
so that every  -vertex cubic graph without a cut-edge has at least
-vertex cubic graph without a cut-edge has at least 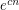 perfect matchings.
perfect matchings. Keywords: cubic; perfect matching
The intersection of two perfect matchings ★★
Conjecture Every bridgeless cubic graph has two perfect matchings 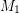 ,
, 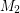 so that
so that 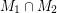 does not contain an odd edge-cut.
does not contain an odd edge-cut.
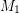 ,
, 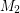 so that
so that 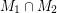 does not contain an odd edge-cut.
does not contain an odd edge-cut. Keywords: cubic; nowhere-zero flow; perfect matching
The Berge-Fulkerson conjecture ★★★★
Conjecture If  is a bridgeless cubic graph, then there exist 6 perfect matchings
is a bridgeless cubic graph, then there exist 6 perfect matchings 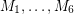 of
of  with the property that every edge of
with the property that every edge of  is contained in exactly two of
is contained in exactly two of 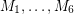 .
.
 is a bridgeless cubic graph, then there exist 6 perfect matchings
is a bridgeless cubic graph, then there exist 6 perfect matchings 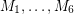 of
of  with the property that every edge of
with the property that every edge of  is contained in exactly two of
is contained in exactly two of 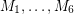 .
.
Keywords: cubic; perfect matching

 Drupal
Drupal CSI of Charles University
CSI of Charles University