 login/create account
login/create account
Linial-Berge path partition duality
Conjecture The minimum  -norm of a path partition on a directed graph
-norm of a path partition on a directed graph  is no more than the maximal size of an induced
is no more than the maximal size of an induced  -colorable subgraph.
-colorable subgraph.
 -norm of a path partition on a directed graph
-norm of a path partition on a directed graph  is no more than the maximal size of an induced
is no more than the maximal size of an induced  -colorable subgraph.
-colorable subgraph. Definitions: Let  be a directed graph. A path partition of
be a directed graph. A path partition of  is a set of vertex disjoint paths in it (some might be singletons), covering all vertices. Let
is a set of vertex disjoint paths in it (some might be singletons), covering all vertices. Let  be a positive integer. The
be a positive integer. The  norm of a path partition is the sum of
norm of a path partition is the sum of 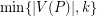 for all paths
for all paths  in it.
in it.
This conjecture is known for acyclic graphs and for 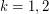 .
.
Thanks Andras!
On September 19th, 2007 mdevos says:
Thanks much for the correction, I've updated the problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Berge-Linial conjecture
There is a typo in the formulation :
Replace "maximum k-norm" by "minimum k-norm".
Thanks ! Best, Andras Sebo