 login/create account
login/create account
Conjecture The minimum  -norm of a path partition on a directed graph
-norm of a path partition on a directed graph  is no more than the maximal size of an induced
is no more than the maximal size of an induced  -colorable subgraph.
-colorable subgraph.
 -norm of a path partition on a directed graph
-norm of a path partition on a directed graph  is no more than the maximal size of an induced
is no more than the maximal size of an induced  -colorable subgraph.
-colorable subgraph. Definitions: Let  be a directed graph. A path partition of
be a directed graph. A path partition of  is a set of vertex disjoint paths in it (some might be singletons), covering all vertices. Let
is a set of vertex disjoint paths in it (some might be singletons), covering all vertices. Let  be a positive integer. The
be a positive integer. The  norm of a path partition is the sum of
norm of a path partition is the sum of 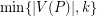 for all paths
for all paths  in it.
in it.
This conjecture is known for acyclic graphs and for 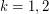 .
.

 Drupal
Drupal CSI of Charles University
CSI of Charles University