 login/create account
login/create account
 be a 3-regular graph that contains no cycle of length shorter than
be a 3-regular graph that contains no cycle of length shorter than 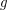 . Is it true that for large enough~
. Is it true that for large enough~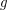 there is a homomorphism
there is a homomorphism 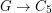 ?
? This question was asked by Nesetril at numerous problem sessions (and also appears as [N]). By Brook's theorem any triangle-free cubic graph is 3-colorable. Does a stronger assumption on girth of the graph imply stronger coloring properties?
This problem is motivated by complexity considerations [GHN] and also by exploration of density of the homomorphism order: We write 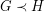 if there is a homomorphism
if there is a homomorphism 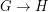 but there is no homomorphism
but there is no homomorphism 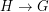 . It is known that whenever
. It is known that whenever 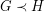 holds and
holds and  ~is not bipartite, there is a graph~
~is not bipartite, there is a graph~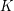 satisfying
satisfying 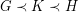 . A negative solution to the Pentagon problem would have the following density consequence: for each cubic graph~
. A negative solution to the Pentagon problem would have the following density consequence: for each cubic graph~ for which~
for which~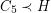 holds, there exists a cubic graph~
holds, there exists a cubic graph~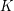 satisfying
satisfying 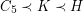 (see [N]).
(see [N]).
If we replaced 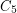 in the statement of the problem by a longer odd cycle, we would get a stronger statement. It is known that no such strenghthening is true. This was proved by Kostochka, Nesetril, and Smolikova [KNS] for
in the statement of the problem by a longer odd cycle, we would get a stronger statement. It is known that no such strenghthening is true. This was proved by Kostochka, Nesetril, and Smolikova [KNS] for 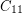 (hence for all
(hence for all 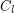 with
with 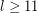 ), by Wanless and Wormald [WW] for
), by Wanless and Wormald [WW] for 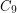 , and recently by Hatami [H] for
, and recently by Hatami [H] for 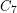 . Each of these results uses probabilistic arguments (random regular graphs), no constructive proof is known.
. Each of these results uses probabilistic arguments (random regular graphs), no constructive proof is known.
Haggkvist and Hell [HH] proved that for every integer~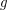 there is a graph~
there is a graph~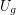 with odd girth at least~
with odd girth at least~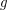 (that is,
(that is, 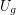 does not contain odd cycle of length less than~
does not contain odd cycle of length less than~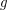 ) such that every cubic graph of odd girth at least~
) such that every cubic graph of odd girth at least~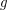 maps homomorphically to~
maps homomorphically to~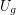 . Here, the graph~
. Here, the graph~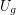 may have large degrees. This leads to a weaker version of the Pentagon problem:
may have large degrees. This leads to a weaker version of the Pentagon problem:
 there exists a cubic graph
there exists a cubic graph 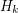 of girth~
of girth~ and an integer~
and an integer~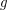 such that every cubic graph of girth at least~
such that every cubic graph of girth at least~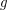 maps homomorphically to~
maps homomorphically to~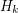 ?
? A particular question in this direction: does a high-girth cubic graph map to the Petersen graph?
As an approach to this, we mention a result of DeVos and Samal [DS]: a cubic graph of girth at least~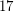 admits a homomorphism to the Clebsch graph. In context of the Pentagon problem, the following reformulation is particularly appealing: If
admits a homomorphism to the Clebsch graph. In context of the Pentagon problem, the following reformulation is particularly appealing: If  ~is a cubic graph of girth at least~
~is a cubic graph of girth at least~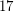 , then there is a cut-continuous mapping from~
, then there is a cut-continuous mapping from~ to~
to~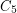 ; that is, there is a mapping
; that is, there is a mapping 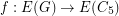 such that for any cut
such that for any cut 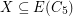 the preimage
the preimage 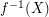 is a cut. (Here by cut we mean the edge-set of a spanning bipartite subgraph. A more thorough exposition of cut-continuous mappings can be found in~[DNR].)
is a cut. (Here by cut we mean the edge-set of a spanning bipartite subgraph. A more thorough exposition of cut-continuous mappings can be found in~[DNR].)
Bibliography
[DNR] Matt DeVos, Jaroslav Nesetril, and Andre Raspaud, On edge-maps whose inverse preverses flows and tensions, Graph Theory in Paris: Proceedings of a Conference in Memory of Claude Berge, Birkhäuser 2006.
[DS] Matt DeVos and Robert Samal, High girth cubic graphs map to the Clebsch graph
[GHN] Anna Galluccio, Pavol Hell, and Jaroslav Nesetril, The complexity of  -colouring of bounded degree graphs, Discrete Math. 222 (2000), no.~1-3, 101--109, MathSciNet
-colouring of bounded degree graphs, Discrete Math. 222 (2000), no.~1-3, 101--109, MathSciNet
[HH] Roland Haggkvist and Pavol Hell, Universality of  -mote graphs, European J. Combin. 14 (1993), no.~1, 23--27.
-mote graphs, European J. Combin. 14 (1993), no.~1, 23--27.
[H] Hamed Hatami, Random cubic graphs are not homomorphic to the cycle of size~7, J. Combin. Theory Ser. B 93 (2005), no.~2, 319--325, MathSciNet
[KNS] Alexandr~V. Kostochka, Jaroslav Nesetril, and Petra Smolikova, Colorings and homomorphisms of degenerate and bounded degree graphs, Discrete Math. 233 (2001), no.~1-3, 257--276, Fifth Czech-Slovak International Symposium on Combinatorics, Graph Theory, Algorithms and Applications, (Prague, 1998), MathSciNet
*[N] Jaroslav Nesetril, Aspects of structural combinatorics (graph homomorphisms and their use), Taiwanese J. Math. 3 (1999), no.~4, 381--423, MathSciNet
[WW] I.M. Wanless and N.C. Wormald, Regular graphs with no homomorphisms onto cycles, J. Combin. Theory Ser. B 82 (2001), no.~1, 155--160, MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University