 login/create account
login/create account
Barnette's Conjecture
(Originally appeared in [B], this discussion appears as [M].)
- \item It is known that this is not true if you remove the "bipartite" condition, but the smallest 3-connected cubic planar graph which is not Hamiltonian has 38 vertices.
\item Holton, Manvel, and McKay [HMM] proved (using computers) that all graphs having fewer than 66 vertices satisfy the conjecture.
\item [A communication by Robert Aldred, Gunnar Brinkmann, and Brendan McKay (December 2002):]
A paper of Holton, Manvel and McKay [HMM] proved Barnette's conjecture for up to 64 vertices, inclusive. This is to announce that the conjecture remains true up to 84 vertices, inclusive. The method used was the same as in the 1985 paper, but took advantage of two developments. One was the new program plantri (Brinkmann and McKay, to be published) which can generate the required graphs without isomorphs at more than 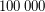 per second. The other was the advance in computers. Total cpu time was about 3 years, almost all of it taken in finding hamiltonian cycles. Specifically, for all 3-connected cubic planar bipartite graphs up to 60 vertices, and those up to 64 vertices not having a 4-face adjacent to two others, we found a hamiltonian cycle using
per second. The other was the advance in computers. Total cpu time was about 3 years, almost all of it taken in finding hamiltonian cycles. Specifically, for all 3-connected cubic planar bipartite graphs up to 60 vertices, and those up to 64 vertices not having a 4-face adjacent to two others, we found a hamiltonian cycle using  and avoiding
and avoiding 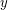 for each pair of edges
for each pair of edges  and
and 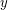 . There are over
. There are over 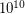 such graphs. By a theorem of Kelman's, one can build a counterexample to Barnette's conjecture when one has a 3-connected cubic planar bipartite graph with this property: for some two edges
such graphs. By a theorem of Kelman's, one can build a counterexample to Barnette's conjecture when one has a 3-connected cubic planar bipartite graph with this property: for some two edges  and
and 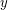 on the same face, there is no hamiltonian cycle that uses
on the same face, there is no hamiltonian cycle that uses  and avoids
and avoids 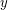 . We did not find any such graph even where
. We did not find any such graph even where  and
and 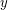 are not required to be on the same face. Perhaps the path to finding a counterexample is to strengthen Kelman's method to some more complicated condition involving 3 or more edges, as then it is more likely to fail on a smaller size.
are not required to be on the same face. Perhaps the path to finding a counterexample is to strengthen Kelman's method to some more complicated condition involving 3 or more edges, as then it is more likely to fail on a smaller size.
There is another conjecture of Barnette (checked by Brendan McKay and Gunnar Brinkmann up to 250 vertices).
Bibliography
*[B] David W. Barnette, Conjecture 5, Recent progress in combinatorics (ed. W. T. Tutte), Academic Press, New York (1969) 343, MathSciNet
[HMM] Derek A.Holton, Bennet Manvel, Brendan D. McKay, Hamiltonian cycles in cubic 3-connected bipartite planar graphs, J. Combin. Theory Ser. B 38 (1985) 279-297. MathSciNet
[M] B. Mohar, Problem of the Month
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Copper Basin Construction
This is nice idea. This is to announce that the conjecture remains true up to 84 vertices, inclusive. The method used was the same as in the 1985 paper, but took advantage of two developments. Thank you.