 login/create account
login/create account
The Erdos-Turan conjecture on additive bases
Let 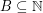 . The representation function
. The representation function 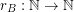 for
for  is given by the rule
is given by the rule 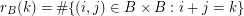 . We call
. We call  an additive basis if
an additive basis if 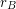 is never
is never  .
.
 is an additive basis, then
is an additive basis, then 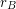 is unbounded.
is unbounded. This famous conjecture seems intuitively likely, but to date, there has been relatively little progress on it despite considerable attention. Two positive results are a theorem of Dirac [D] which shows that 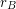 cannot be constant from some point on, and a theorem of Borwein, Choi, and Chu [BCC] which shows that
cannot be constant from some point on, and a theorem of Borwein, Choi, and Chu [BCC] which shows that 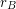 cannot be bounded above by
cannot be bounded above by  .
.
On the other hand, if we consider the related problem for subsets of integers instead of natural numbers, Nathanson [N] has shown that the conjecture does not hold.
Bibliography
[BCC] P. Borwein, S. Choi, and F. Chu, An old conjecture of Erdos-Turan on additive bases, Mathematics of Computation. Volume 75, Number 253, Pages 475–484.
[D] G. A. Dirac, Note on a problem in additive number theory, J. London Math. Soc. 26 (1951), 312–313.
[EG] P. Erdos and R. L. Graham, Old and new problems and results in combinatorial number theory: van der Waerden’s theorem and related topics, Enseign. Math. (2) 25 (1979), no. 3-4, 325–344 (1980). MathSciNet
*[ET] P. Erdos and P. Turan, On a problem of Sidon in additive number theory, and on some related problems, J. London Math. Soc. 16 (1941), 212–215. MathSciNet
[N] Melvyn B. Nathanson, Unique representation bases for the integers, Acta Arith. 108 (2003), no. 1, 1–8. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University