 login/create account
login/create account
Saturated $k$-Sperner Systems of Minimum Size
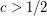 and a function
and a function 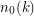 such that if
such that if 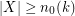 , then every saturated
, then every saturated  -Sperner system
-Sperner system  has cardinality at least
has cardinality at least 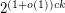 ?
? The power set of a set 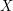 , denoted
, denoted 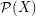 , is the collection of all subsets of
, is the collection of all subsets of 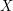 . A collection
. A collection 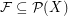 is said to be a
is said to be a  -Sperner system if there does not exist a subcollection
-Sperner system if there does not exist a subcollection 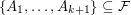 such that
such that 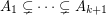 ; such a subcollection is called a
; such a subcollection is called a 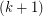 -chain. A
-chain. A  -Sperner system
-Sperner system 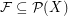 is said to be saturated if for every subset
is said to be saturated if for every subset  of
of 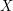 not contained in
not contained in 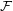 , the collection
, the collection 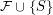 contains a
contains a 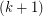 -chain.
-chain.
Gerbner et al. [1] proved that if 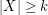 , then every saturated
, then every saturated  -Sperner System in
-Sperner System in 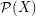 has cardinality at least
has cardinality at least 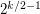 . Moreover, they conjectured that there exists a function
. Moreover, they conjectured that there exists a function 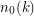 such that if
such that if 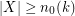 , then the minimum size of a saturated
, then the minimum size of a saturated  -Sperner System in
-Sperner System in 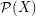 has size
has size 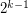 . This was disproved by Morrison, Noel and Scott in [2], who showed the following:
. This was disproved by Morrison, Noel and Scott in [2], who showed the following:
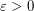 and a function
and a function 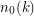 such that for every
such that for every  and every set
and every set 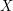 such that
such that 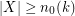 there exists a saturated
there exists a saturated  -Sperner system in
-Sperner system in 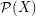 of cardinality at most
of cardinality at most 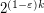 .
. The value of  which can be deduced from their proof is approximately
which can be deduced from their proof is approximately 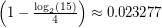 . Moreover, in [2] it was shown that there exists a function
. Moreover, in [2] it was shown that there exists a function 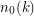 and a constant
and a constant ![$ c\in [1/2,1-\varepsilon] $](/files/tex/3012e181c3d325589681f7b793b48e1a3bb4c120.png) such that if
such that if 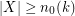 , then the size of the smallest
, then the size of the smallest  -Sperner System in
-Sperner System in 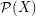 is asymptotically
is asymptotically 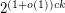 . The problem stated here is to determine whether
. The problem stated here is to determine whether 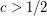 .
.
A 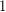 -Sperner system is called an antichain. As was observed in [2], a positive answer to the above question would follow from a positive answer to the following question:
-Sperner system is called an antichain. As was observed in [2], a positive answer to the above question would follow from a positive answer to the following question:
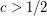 and a function
and a function 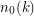 such that if
such that if 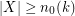 and
and 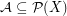 is a saturated antichain in which every element of
is a saturated antichain in which every element of 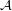 has cardinality between
has cardinality between 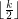 and
and 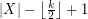 , then
, then 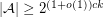 ?
? A more general problem is the following:
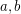 and a set
and a set 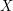 , what is the minimum size of a saturated antichain
, what is the minimum size of a saturated antichain 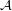 in
in 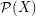 in which every set of
in which every set of 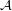 has cardinality between
has cardinality between  and
and 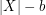 ?
? Bibliography
[1] D. Gerbner, B. Keszegh, N. Lemons, C. Palmer, D. Palvolgyi, and B. Patkos, Saturating Sperner Families, Graphs Combin. 29 (2013), no. 5, 1355–1364. arXiv:1105.4453
*[2] N. Morrison, J. A. Noel, A. Scott. On Saturated k-Sperner Systems. arXiv:1402.5646 (2014). arXiv:1402.5646
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University