 login/create account
login/create account
Sperner system
Saturated $k$-Sperner Systems of Minimum Size ★★
Author(s): Morrison; Noel; Scott
Question Does there exist a constant 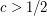 and a function
and a function 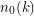 such that if
such that if 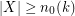 , then every saturated
, then every saturated  -Sperner system
-Sperner system  has cardinality at least
has cardinality at least 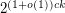 ?
?
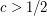 and a function
and a function 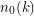 such that if
such that if 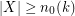 , then every saturated
, then every saturated  -Sperner system
-Sperner system  has cardinality at least
has cardinality at least 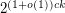 ?
? Keywords: antichain; extremal combinatorics; minimum saturation; saturation; Sperner system

 Drupal
Drupal CSI of Charles University
CSI of Charles University