 login/create account
login/create account
Edge-disjoint Hamilton cycles in highly strongly connected tournaments.
Conjecture For every 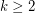 , there is an integer
, there is an integer 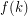 so that every strongly
so that every strongly 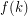 -connected tournament has
-connected tournament has  edge-disjoint Hamilton cycles.
edge-disjoint Hamilton cycles.
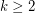 , there is an integer
, there is an integer 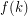 so that every strongly
so that every strongly 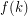 -connected tournament has
-connected tournament has  edge-disjoint Hamilton cycles.
edge-disjoint Hamilton cycles. Kelly made the following conjecture which replaces the assumption of high connectivity by regularity.
Conjecture Every regular tournament of order  can be decomposed into
can be decomposed into 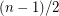 Hamilton directed cycles.
Hamilton directed cycles.
 can be decomposed into
can be decomposed into 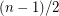 Hamilton directed cycles.
Hamilton directed cycles. Kelly's conjecture has been proved for tournaments of sufficiently large order by Kühn and Osthus [KO].
Bibliography
[KO] Daniela Kühn and Deryk Osthus, Hamilton decompositions of regular expanders: a proof of Kelly's conjecture for large tournaments, Advances in Mathematics 237 (2013), 62-146.
*[T] C. Thomassen, Edge-disjoint Hamiltonian paths and cycles in tournaments, Proc. London Math. Soc. 45 (1982), 151-168.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University