 login/create account
login/create account
Decomposing an even tournament in directed paths.
 on an even number of vertices can be decomposed into
on an even number of vertices can be decomposed into 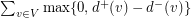 directed paths.
directed paths. This conjecture is clearly tight, because in a decomposition of a directed graph in directed paths, at least 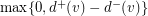 directed paths must start at vertex
directed paths must start at vertex  .
.
Observe that the analogue is trivially false for odd tournament: in regular tournament 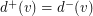 for every vertex
for every vertex  , so
, so 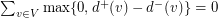 . For a tournament of even order
. For a tournament of even order  ,
, 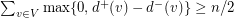 . Since a directed path may have up to
. Since a directed path may have up to 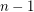 arcs, it might be possible to cover the
arcs, it might be possible to cover the 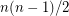 arcs of the tournament if
arcs of the tournament if  is even. If the tournament is almost regular (i.e.
is even. If the tournament is almost regular (i.e. 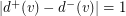 for all vertex
for all vertex  ), the conjecture asserts that it can be decomposed into directed Hamilton paths.
), the conjecture asserts that it can be decomposed into directed Hamilton paths.
This conjecture for almost regular tournaments would imply the following one due to Kelly.
 can be decomposed into
can be decomposed into 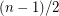 Hamilton directed cycles.
Hamilton directed cycles. To see this, consider a regular tournament  and a vertex
and a vertex  of
of  . The tournament
. The tournament 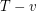 has even order, and in
has even order, and in 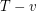 ,
, 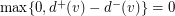 unless
unless  is an outneighbour of
is an outneighbour of  in
in  in which case
in which case 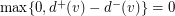 . Hence
. Hence 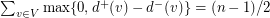 . Now if Alspach-Mason-Pulman conjecture holds,
. Now if Alspach-Mason-Pulman conjecture holds, 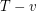 can be decomposed into
can be decomposed into 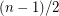 directed paths. These paths must start at distinct outneighbours of
directed paths. These paths must start at distinct outneighbours of  in
in  and ends at distinct inneighbours of
and ends at distinct inneighbours of  in
in  . Hence, we can complete each directed path in a Hamilton directed cycle in
. Hence, we can complete each directed path in a Hamilton directed cycle in  to obtain a decomposition of
to obtain a decomposition of  into
into 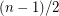 Hamilton cycles.
Hamilton cycles.
Kelly's conjecture has been proved for tournaments of sufficiently large order by Kühn and Osthus [KO].
Bibliography
*[AMP] Brian Alspach, David W. Mason, Norman J. Pullman, Path numbers of tournaments, Journal of Combinatorial Theory, Series B, 20 (1976), no. 3, June 1976, 222–228
[KO] Daniela Kühn and Deryk Osthus, Hamilton decompositions of regular expanders: a proof of Kelly's conjecture for large tournaments, Advances in Mathematics 237 (2013), 62-146.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University