Home » Subject » Graph Theory » Basic G.T.
Importance: Medium ✭✭
Author(s): Thomassen, Carsten
Subject: Graph Theory
» Basic Graph Theory
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: March 5th, 2013
Conjecture   For all positive integers $ g $ and $ k $, there exists an integer $ d $ such that every graph of average degree at least $ d $ contains a subgraph of average degree at least $ k $ and girth greater than $ g $.

This conjecture is true for regular graphs as observed by Alon (see [KO]). The case 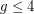$ g\leq 4 $ was proved in [KO].

Bibliography

[KO] D. Kühn and D. Osthus, Every graph of sufficiently large average degree contains a C4-free subgraph of large average degree, Combinatorica, 24 (2004), 155-162.

*[T] C. Thomassen, Girth in graphs, J. Combin. Theory B 35 (1983), 129–141.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options