 login/create account
login/create account
Counting 3-colorings of the hex lattice
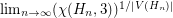 .
. We'll begin by putting in place the necessary notation. Let  be the regular triangular tiling of the plane. For every
be the regular triangular tiling of the plane. For every  there is a regular map which triangulates the torus, denoted
there is a regular map which triangulates the torus, denoted  , which may be obtained from a regular hexagonal piece of
, which may be obtained from a regular hexagonal piece of 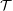 of side-length
of side-length  by identifying points on opposite edges of this hexagon. Let
by identifying points on opposite edges of this hexagon. Let 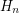 be the dual of
be the dual of 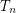 (on the torus). Then
(on the torus). Then 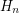 is a regular map on the torus - a hexagonal tiling. One last definition: for any graph
is a regular map on the torus - a hexagonal tiling. One last definition: for any graph  and any positive integer
and any positive integer  we let
we let 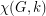 denote the number of proper
denote the number of proper  -coloring of
-coloring of  .
.
A famous theorem of Lieb [L] shows that 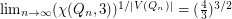 where
where 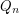 denotes the
denotes the 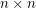 quadrangulation of the torus. This theorem is usually stated in terms of Eulerian orientations, and is of interest to physicists as the constant
quadrangulation of the torus. This theorem is usually stated in terms of Eulerian orientations, and is of interest to physicists as the constant 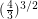 (called Lieb's Ice Constant) determines the "residual entropy for square ice".
(called Lieb's Ice Constant) determines the "residual entropy for square ice".
Thomassen proved that every planar graph  with girth
with girth 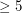 has exponentially many proper 3-colorings. More precisely, he showed that
has exponentially many proper 3-colorings. More precisely, he showed that 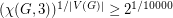 . This gives a lower bound on the limit in the above problem (assuming it exists).
. This gives a lower bound on the limit in the above problem (assuming it exists).
Bibliography
[L] E. H. Lieb, Exact Solution of the Problem of the Entropy of Two-Dimensional Ice. Phys. Rev. Lett. 18, 692-694, 1967.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University