 login/create account
login/create account
Partitionning a tournament into k-strongly connected subtournaments.
 be positve integer Does there exists an integer
be positve integer Does there exists an integer 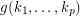 such that every
such that every 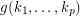 -strong tournament
-strong tournament  admits a partition
admits a partition 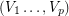 of its vertex set such that the subtournament induced by
of its vertex set such that the subtournament induced by 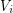 is a non-trivial
is a non-trivial 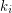 -strong for all
-strong for all 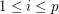 .
. If 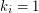 for
for 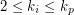 , then
, then 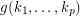 exists and is at most
exists and is at most 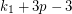 . This follows by an easy induction on
. This follows by an easy induction on  , by taking
, by taking 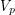 to be a set inducing a directed
to be a set inducing a directed  -cycle.
-cycle.
The following example shows that if it exists 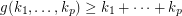 . Set
. Set 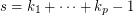 . For
. For 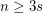 , let
, let  be a tournament on
be a tournament on  vertices having a set
vertices having a set 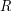 of
of  vertices such that
vertices such that 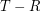 a transitive tournament of order
a transitive tournament of order  with hamiltonian path
with hamiltonian path 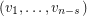 , and
, and 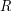 dominates
dominates  and is dominated by
and is dominated by 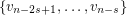 . It easy to check that
. It easy to check that  is
is  -strongly connected. However, every (non-trivial)
-strongly connected. However, every (non-trivial)  -strong tournament of
-strong tournament of  must contain at least
must contain at least  vertices of
vertices of 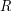 . Hence
. Hence  does not have a partition
does not have a partition 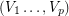 of its vertex set such that the subtournament induced by
of its vertex set such that the subtournament induced by 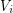 is a non-trivial
is a non-trivial 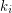 -strong for all
-strong for all 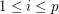 .
.
Some small examples give better lower bound. For example, the Paley tournament on 7 vertices which is 3-strong cannot be partionned into two strong subtournaments. However, there are only finitely many known such tournaments. Chen, Gould, and Li [CGL] showed that every  -strongly connected tournament with at least
-strongly connected tournament with at least 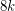 vertices has a partition into
vertices has a partition into  strongly connected tournaments.
strongly connected tournaments.
The existence of 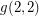 is still open.
is still open.
Bibliography
[CGL] G. Chen, R.J. Gould, and H. Li, Partitioning vertices of a tournament into independent cycles, J. combin. Theory Ser B, Vol 83, no. 2 (2001) 213-220.
*[R] K.B. Reid, Three problems on tournaments, Graph Theory and Its Applications, East. and West. Ann. New York Acad. Sci. 576 (1989), 466-473.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University