Home » Subject » Graph Theory » Directed Graphs
Importance: Medium ✭✭
Author(s): Thomassen, Carsten
Subject: Graph Theory
» Directed Graphs
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: March 2nd, 2013
Conjecture   There exists an integer $ k $ such that every $ k $-arc-strong digraph $ D $ with specified vertices $ u $ and $ v $ contains an out-branching rooted at $ u $ and an in-branching rooted at $ v $ which are arc-disjoint.

Thomassen [T] showed that, given a digraph $ D $ and two vertices $ u $ and $ v $, deciding whether there are an out-branching rooted at $ u $ and an in-branching rooted at $ v $ which are arc-disjoint is NP-complete.

In contrast, one can decide in polynomial time whether there are $ k $ arc-disjoint out-branchings with specified roots 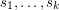$ s_1, \dots , s_k $ (some of which may be identical). This is a consequence of Edmonds’ well known branching theorem [E] states that a digraph $ D $ has $ k $ arc-disjoint out-branchings rooted at some fixed vertex $ s $ if and only if there are $ k $ arc-disjoint paths from $ s $ to every other vertex of $ D $.

Bang-Jensen [B] proved this conjecture for tournaments.

A similar question can be asked about arc-disjoint strongly connected spanning subdigraphs. Several related problems are mentioned in the survey of Bang-Jensen and Kriesell [BK].

Related problems

Arc-disjoint strongly connected spanning subdigraphs

Bibliography

[B] J. Bang-Jensen, Edge-disjoint in- and out-branching in tournaments and related path problems. J. Combin. Theory Ser. B 51 (1991), 1-23.

[BK] J. Bang-Jensen, M. Kriesell, Disjoint sub(di)graphs in digraphs, Electronic Notes in Discrete Mathematics 34 (2009), 179-183.

[E] J. Edmonds, Edge-disjoint branchings. In Combinatorial Algorithms, B. Rustin, ed., Acad. Press, New York (1973), 91-96.

*[T] C. Thomassen, Configurations in Graphs, Annals of The New York Acad. Sci. 555 (1989), 402-412.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options