 login/create account
login/create account
Sabidussi, Gert
Decomposing an eulerian graph into cycles with no two consecutives edges on a prescribed eulerian tour. ★★
Author(s): Sabidussi
Conjecture Let  be an eulerian graph of minimum degree
be an eulerian graph of minimum degree  , and let
, and let 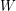 be an eulerian tour of
be an eulerian tour of  . Then
. Then  admits a decomposition into cycles none of which contains two consecutive edges of
admits a decomposition into cycles none of which contains two consecutive edges of 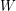 .
.
 be an eulerian graph of minimum degree
be an eulerian graph of minimum degree  , and let
, and let 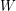 be an eulerian tour of
be an eulerian tour of  . Then
. Then  admits a decomposition into cycles none of which contains two consecutive edges of
admits a decomposition into cycles none of which contains two consecutive edges of 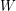 .
. Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University