 login/create account
login/create account
Decomposing eulerian graphs
 is a 6-edge-connected Eulerian graph and
is a 6-edge-connected Eulerian graph and  is a 2-transition system for
is a 2-transition system for  , then
, then 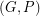 has a compaible decomposition.
has a compaible decomposition. Definition: Let  be an Eulerian graph and for every vertex
be an Eulerian graph and for every vertex  , let
, let 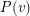 be a partition of the edges incident with
be a partition of the edges incident with  . We call
. We call  a transition system. If every member of
a transition system. If every member of 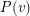 has size at most
has size at most  (for every
(for every  ), then we call
), then we call  a
a  -transition sytem. A compatible decomposition of
-transition sytem. A compatible decomposition of 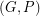 is a list of edge-disjoint cycles
is a list of edge-disjoint cycles 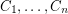 with union
with union  so that every
so that every 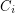 contains at most one edge from every member of
contains at most one edge from every member of 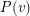 .
.
Let  be a graph and let
be a graph and let 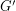 be the graph obtained from
be the graph obtained from  by replacing each edge
by replacing each edge  of G by two edges
of G by two edges 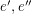 in parallel. Let
in parallel. Let  be the 2-transition system of
be the 2-transition system of  with
with 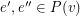 whenever
whenever 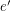 and
and 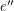 are incident with
are incident with  . Now,
. Now, 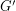 is an Eulerian graph and every compatible decomposition of
is an Eulerian graph and every compatible decomposition of 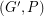 gives a cycle double cover of
gives a cycle double cover of  . Since the cycle double cover conjecture can be reduced to graphs which are 3-edge-connected, the above conjecture would imply the cycle double cover conjecture.
. Since the cycle double cover conjecture can be reduced to graphs which are 3-edge-connected, the above conjecture would imply the cycle double cover conjecture.
We define a transition system  to be admissable if every member of
to be admissable if every member of 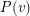 contains no more than half of the edges in any edge-cut. It is easy to see that if there is a compatible decomposition of
contains no more than half of the edges in any edge-cut. It is easy to see that if there is a compatible decomposition of 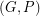 , then
, then  must be admissable. The converse of this is not true; There is an admissable 2-transition system of the graph
must be admissable. The converse of this is not true; There is an admissable 2-transition system of the graph 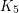 which does not admit a compatible decomposition. Recently, G. Fan and C.Q. Zhang [FZ] have proved that
which does not admit a compatible decomposition. Recently, G. Fan and C.Q. Zhang [FZ] have proved that 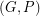 does have a compatible decomposition whenever
does have a compatible decomposition whenever  is admissable and
is admissable and  has no
has no 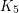 minor. This result imporoved upon an earlier theorem of Fleischner and Frank [FF]. Very recently, I have proved a weak version of the above conjecture, by showing that
minor. This result imporoved upon an earlier theorem of Fleischner and Frank [FF]. Very recently, I have proved a weak version of the above conjecture, by showing that 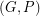 also has a compatible decomposition when P is a 2-transition system and G is 80-edge-connected. I'd quite like to see an improvement on this bound. Here is a related conjecture.
also has a compatible decomposition when P is a 2-transition system and G is 80-edge-connected. I'd quite like to see an improvement on this bound. Here is a related conjecture.
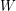 be an Euler tour of the graph
be an Euler tour of the graph  . If
. If  has no vertex of degree two, then there is a cycle decomposition of
has no vertex of degree two, then there is a cycle decomposition of  , say
, say 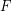 , so that no two consecutive edges of
, so that no two consecutive edges of 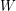 are in a common circuit of
are in a common circuit of 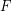 .
. If 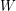 is given by
is given by 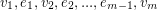 then we may form a 2-transition system
then we may form a 2-transition system  by putting
by putting 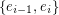 in
in 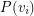 for every
for every  (working modulo
(working modulo  ). Now a compatible decomposition of
). Now a compatible decomposition of 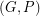 is precisely a cycle decomposition of
is precisely a cycle decomposition of  satisfying the above conjecture. Thus, Sabidussi's conjecture is equivalent to the assertion that
satisfying the above conjecture. Thus, Sabidussi's conjecture is equivalent to the assertion that 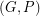 has a compatible decomposition whenever
has a compatible decomposition whenever  has no vertex of degree two and
has no vertex of degree two and  is a 2-transition system which comes from an Euler tour.
is a 2-transition system which comes from an Euler tour.
Let  be a directed Eulerian graph and for every vertex
be a directed Eulerian graph and for every vertex  , let
, let 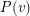 be a partition of the edges incident with
be a partition of the edges incident with  into pairs so that every in-edge is paired with an out-edge. We define a compatible decomposition to be a decomposition of
into pairs so that every in-edge is paired with an out-edge. We define a compatible decomposition to be a decomposition of  into directed circuits so that every directed circuit contains at most one edge from every member of
into directed circuits so that every directed circuit contains at most one edge from every member of 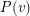 . Our current techniques don't seem to shed any light on the problem of finding compatible decompositions for Eulerian digraphs. Next I pose a very basic question which is still open.
. Our current techniques don't seem to shed any light on the problem of finding compatible decompositions for Eulerian digraphs. Next I pose a very basic question which is still open.
 such that
such that 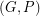 has a compatible decomposition whenever
has a compatible decomposition whenever  is a
is a  -edge-connected directed Eulerian graph and
-edge-connected directed Eulerian graph and  is a 2-transition system?
is a 2-transition system? 
 Drupal
Drupal CSI of Charles University
CSI of Charles University