 login/create account
login/create account
Hamiltonicity of Cayley graphs
This problem seems to have been first considered by Rapaport-Strasser [R]. Lovasz [L] conjectured more generally that every vertex-transitive graph is Hamiltonian. For a survey of results up to 1996, see [CG]. Although many specific Cayley graphs have been shown to be Hamiltonian, there are few general results. One exception is the theorem by Pak and Radoičić [PR] that every finite group  with at least three elements has a generating set
with at least three elements has a generating set  of size
of size 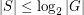 , such that the corresponding Cayley graph is Hamiltonian.
, such that the corresponding Cayley graph is Hamiltonian.
Bibliography
[CG] S. J. Curran, J. A. Gallian, Hamiltonian cycles and paths in Cayley graphs and digraphs—a survey, Discrete Math. 156 (1996), 1–18.
[L] L. Lovasz, Problem 11, in “Combinatorial structures and their applications,” University of Calgary, Calgary, Alberta, Canada (1970), Gordon and Breach, New York.
[PR] I. Pak and R. Radoičić, Hamiltonian paths in Cayley graphs, preprint.
*[R] E. Rapaport-Strasser, Cayley color groups and Hamilton lines, Scripta Math. 24 (1959), 51–58.
* indicates original appearance(s) of problem.
[PR] paper
First, link to PR paper has moved with Pak homepage. Second, it is now published in Discrete Math.
Is this at all relevant?
Not sure but wondering if this link is at all relevant to the problem:
http://books.google.com/books?id=aSyXqtfOuU4C&pg=PA49&dq=Cayley+graph&num=100&client=firefox-a#PPA49,M1
Thanks,
- Farley
graphs vs. digraphs
The book you link to has examples of directed Cayley graphs with no (directed) Hamiltonian cycle. The existence of such graphs is interesting and relevant, but does not give a counterexample to the problem stated here.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Hamiltonicity of dence Cayley graphs
Christofides, Hladky, and Mathe (http://arxiv.org/abs/1008.2193) proved using the Regularity Method the case when the vertex-transitive graph is sufficiently dense.