 login/create account
login/create account
This problem seems to have been first considered by Rapaport-Strasser [R]. Lovasz [L] conjectured more generally that every vertex-transitive graph is Hamiltonian. For a survey of results up to 1996, see [CG]. Although many specific Cayley graphs have been shown to be Hamiltonian, there are few general results. One exception is the theorem by Pak and Radoičić [PR] that every finite group  with at least three elements has a generating set
with at least three elements has a generating set  of size
of size 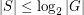 , such that the corresponding Cayley graph is Hamiltonian.
, such that the corresponding Cayley graph is Hamiltonian.
Bibliography
[CG] S. J. Curran, J. A. Gallian, Hamiltonian cycles and paths in Cayley graphs and digraphs—a survey, Discrete Math. 156 (1996), 1–18.
[L] L. Lovasz, Problem 11, in “Combinatorial structures and their applications,” University of Calgary, Calgary, Alberta, Canada (1970), Gordon and Breach, New York.
[PR] I. Pak and R. Radoičić, Hamiltonian paths in Cayley graphs, preprint.
*[R] E. Rapaport-Strasser, Cayley color groups and Hamilton lines, Scripta Math. 24 (1959), 51–58.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University