 login/create account
login/create account
(m,n)-cycle covers
Definition: If 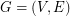 is a graph, a binary cycle of
is a graph, a binary cycle of  is a set
is a set 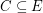 such that every vertex of the graph
such that every vertex of the graph 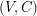 has even degree. An
has even degree. An 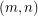 -cycle-cover of
-cycle-cover of  is a list
is a list 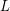 consisting of
consisting of  cycles so that every edge of
cycles so that every edge of  is contained in exactly
is contained in exactly  of these cycles.
of these cycles.
Since every binary cycle can be written as a disjoint union of edge sets of ordinary cycles, the above conjecture is a strengthening of the cycle double cover conjecture. For positive integers 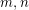 it is natural to ask what family of graphs have
it is natural to ask what family of graphs have 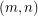 -cycle-covers. The following chart gives some information about this question for small values of
-cycle-covers. The following chart gives some information about this question for small values of  and
and  . A "yes" in the
. A "yes" in the 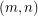 box indicates that every graph with no cut-edge has an
box indicates that every graph with no cut-edge has an 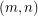 -cycle-cover. A "no" indicates that no graph has an
-cycle-cover. A "no" indicates that no graph has an 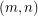 -cycle-cover. A more detailed explanation of the entries in this chart appears below it.
-cycle-cover. A more detailed explanation of the entries in this chart appears below it.
| m | |||||||||||||||||||||||||||||||||||||||||||||
| n |
| ||||||||||||||||||||||||||||||||||||||||||||
We did not include odd values of n, since any graph with an 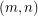 -cycle-cover for an odd integer
-cycle-cover for an odd integer  must be Eulerian. The entry "NZ 4-flow" is short for nowhere-zero 4-flow. Thus, our chart indicates that (
must be Eulerian. The entry "NZ 4-flow" is short for nowhere-zero 4-flow. Thus, our chart indicates that ( has a nowhere-zero 4-flow) if and only if (
has a nowhere-zero 4-flow) if and only if ( has a
has a 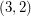 -cycle-cover) if and only if (
-cycle-cover) if and only if ( has a
has a 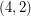 -cycle-cover). These equivalences were discovered by Tutte [Tu].
-cycle-cover). These equivalences were discovered by Tutte [Tu].
Two of the 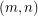 boxes are conjectures. The 5CDC conj is the 5 cycle double cover conjecture and the B-F conjecture is the Berge-Fulkerson conjecture. In both of these cases, the conjecture is equivalent to the assertion that every graph with no cut-edge has an
boxes are conjectures. The 5CDC conj is the 5 cycle double cover conjecture and the B-F conjecture is the Berge-Fulkerson conjecture. In both of these cases, the conjecture is equivalent to the assertion that every graph with no cut-edge has an 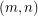 -cycle-cover (i.e. it would be accurate to put a "yes" in the corresponding. box). For emphasis, we state the Berge-Fulkerson conjecture again below in this new form.
-cycle-cover (i.e. it would be accurate to put a "yes" in the corresponding. box). For emphasis, we state the Berge-Fulkerson conjecture again below in this new form.
The fact that the above conjecture is equivalent to the usual statement of the Berge-Fulkerson conjecture was discovered by Jaeger [J]. For cubic graphs this equivalence is easy to see, since 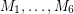 satisfy the Berge-Fulkerson conjecture if and only if
satisfy the Berge-Fulkerson conjecture if and only if 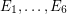 is a
is a 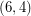 -cycle-cover. By Jaeger's argument, the weak Berge-Fulkerson conjecture is equivalent to the statement that there exists a fixed integer
-cycle-cover. By Jaeger's argument, the weak Berge-Fulkerson conjecture is equivalent to the statement that there exists a fixed integer  so that every bridgeless graph has a
so that every bridgeless graph has a 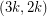 -cycle-cover.
-cycle-cover.
A postman set is a set of edges 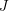 such that
such that 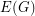 is a cycle. The entry "k post. sets" in the
is a cycle. The entry "k post. sets" in the 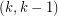 box of the above chart indicates that a graph G has a
box of the above chart indicates that a graph G has a 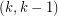 -cycle-cover if and only if it is possible to partition the edges of
-cycle-cover if and only if it is possible to partition the edges of  into
into  postman sets. This equivalence follows immediately from the definition. Rizzi's Packing postman sets conjecture is thus equivalent to the following conjecture on cycle-covers.
postman sets. This equivalence follows immediately from the definition. Rizzi's Packing postman sets conjecture is thus equivalent to the following conjecture on cycle-covers.
 has size
has size 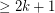 , then
, then  has a
has a 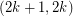 -cycle-cover.
-cycle-cover. Next we turn our attention to orientable cycle covers. If  is a directed graph a map
is a directed graph a map 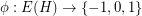 is a 2-flow or an oriented cycle if at every vertex of
is a 2-flow or an oriented cycle if at every vertex of  , the sum of
, the sum of 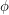 on the incoming edges is equal to the sum of
on the incoming edges is equal to the sum of 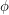 on the outgoing edges. It is easy to see that the support of a 2-flow is always a cycle. Furthermore, for any oriented cycle, there is a list
on the outgoing edges. It is easy to see that the support of a 2-flow is always a cycle. Furthermore, for any oriented cycle, there is a list 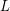 of edge-disjoint circuits with directions so that an edge
of edge-disjoint circuits with directions so that an edge  is forward (backward) in a circuit of
is forward (backward) in a circuit of 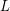 if and only if
if and only if 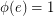 (
(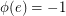 ). So as in the unoriented case, an oriented cycle may be viewed as the edge-disjoint union of oriented circuits. For an even integer
). So as in the unoriented case, an oriented cycle may be viewed as the edge-disjoint union of oriented circuits. For an even integer  , a
, a 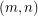 -oriented-cycle-cover of a graph
-oriented-cycle-cover of a graph  is a list of
is a list of  oriented cycles so that every edge of
oriented cycles so that every edge of  appears as a forward edge
appears as a forward edge 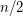 times and a backward edge
times and a backward edge 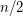 times. The following conjecture is the common generalization of the orientable cycle double cover conjecture and the five cycle double cover conjecture. It is due to Archdeacon and Jaeger.
times. The following conjecture is the common generalization of the orientable cycle double cover conjecture and the five cycle double cover conjecture. It is due to Archdeacon and Jaeger.
Considerably less is known about 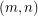 -oriented-cycle-covers. We sumarize some of what is known for small values of
-oriented-cycle-covers. We sumarize some of what is known for small values of  and
and  below.
below.
| m | ||||||||||||||||||||||||||||||||||||||||||||||
| n |
| |||||||||||||||||||||||||||||||||||||||||||||
Every graph with an 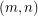 -cycle-cover also has a
-cycle-cover also has a 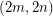 -oriented-cycle-cover obtained by taking two copies of each cycle with opposite orientations. Thus, by Bermond, Jackson, and Jaeger's
-oriented-cycle-cover obtained by taking two copies of each cycle with opposite orientations. Thus, by Bermond, Jackson, and Jaeger's 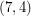 -cycle-cover theorem, every bridgeless graph with no has a
-cycle-cover theorem, every bridgeless graph with no has a 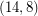 -oriented-cycle-cover. DeVos and Goddyn have observed that Seymour's 6-flow theorem can be used to construct an
-oriented-cycle-cover. DeVos and Goddyn have observed that Seymour's 6-flow theorem can be used to construct an 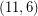 -oriented-cycle-cover for every bridgeless graph. By combining these, we find that for every even integer
-oriented-cycle-cover for every bridgeless graph. By combining these, we find that for every even integer 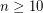 there exists an
there exists an  so that every bridgeless graph has an
so that every bridgeless graph has an 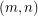 -oriented-cycle-cover. This question is still open for
-oriented-cycle-cover. This question is still open for 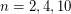 .
.
The following conjecture appears in the above chart.
This conjecture may be viewed as a sort of oriented version of the Berge-Fulkerson conjecture. To see this analogy, note that ( has a nowhere-zero 4-flow) if and only if (
has a nowhere-zero 4-flow) if and only if ( has a
has a 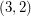 -cycle-cover) if and only if (
-cycle-cover) if and only if ( has a
has a 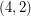 -oriented-cycle-cover). The Berge-Fulkerson conjecture and the above conjecture assert respectively that every bridgeless graph has a
-oriented-cycle-cover). The Berge-Fulkerson conjecture and the above conjecture assert respectively that every bridgeless graph has a 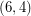 -cycle-cover and a
-cycle-cover and a 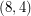 -oriented-cycle-cover (i.e. a cover with double the parameters which are equivalent to a nowhere-zero 4-flow). As with most of the conjectures in this area, the above conjecture is trivially true for graphs with nowhere-zero 4-flows and it holds for the Petersen graph.
-oriented-cycle-cover (i.e. a cover with double the parameters which are equivalent to a nowhere-zero 4-flow). As with most of the conjectures in this area, the above conjecture is trivially true for graphs with nowhere-zero 4-flows and it holds for the Petersen graph.
Bibliography
[A] D. Archdeacon, Face coloring of embedded graphs. J. Graph Theory, 8(1984), 387-398.
[BJJ] J.C. Bermond, B. Jackson, and F. Jaeger, Shortest covering of graphs with cycles, J. Combinatorial Theory Ser. B 35 (1983), 297-308. MathSciNet
*[C] A. U. Celmins, On cubic graphs that do not have an edge-3-colouring, Ph.D. Thesis, Department of Combinatorics and Optimization, University of Waterloo, Waterloo, Canada, 1984.
[F] G. Fan, Integer flows and cycle covers, J. Combinatorial Theory Ser. B 54 (1992), 113-122. MathSciNet
[J] F. Jaeger, Flows and Generalized Coloring Theorems in Graphs, J. Combinatorial Theory Ser. B 26 (1979) 205-216. MathSciNet
[J88] F. Jaeger, Nowhere zero flow problems. Selected Topics in Graph Theory 3 (L.W.Beineke and R.J.Wilson eds.), Academic Press, London (1988), 71-95.
*[P] M. Preissmann, Sur les colorations des arêtes des graphes cubiques, Thèse de 3ème cycle, Grenoble (1981) .
[T54] W.T. Tutte, A Contribution on the Theory of Chromatic Polynomials, Canad. J. Math. 6 (1954) 80-91. MathSciNet
[T66] W.T. Tutte, On the Algebraic Theory of Graph Colorings, J. Combinatorial Theory 1 (1966) 15-50. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University