Home » Subject » Graph Theory » Infinite Graphs
Importance: Medium ✭✭
Author(s): Georgakopoulos, Agelos
Subject: Graph Theory
» Infinite Graphs
Keywords: hamiltonian
infinite graph
line graphs
Recomm. for undergrads: no
Posted by: Robert Samal
on: July 24th, 2007
Conjecture  
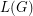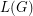    \item If $ G $ is a 4-edge-connected locally finite graph, then its line graph is hamiltonian. \item If the line graph $ L(G) $ of a locally finite graph $ G $ is 4-connected, then $ L(G) $ is hamiltonian.

(Reproduced from [M].)

A locally finite graph is hamiltonian, if its Freudenthal compactification (also called the end compactification, see [D]) contains a hamilton circle, i.e. a homeomorphic copy of 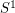$ S^1 $ containing all vertices.

The first part is known for finite graphs. The proof uses the existence of two edge-disjoint spanning trees in 4-edge-connected graphs. In the infinite case, it would be enough to prove that a 4-edge-connected locally finite graph $ G $ has two edge-disjoint topological spanning trees (see [D]), one of which is connected as a subgraph of $ G $. The problem is open even for the 1-ended case (where hamilton circles correspond to 2-way-infinite paths).

The second part is widely open even in the finite case, where it was proposed by Thomassen [T].

Related problems

Hamiltonian cycles in line graphs

Bibliography

[D] Reinhard Diestel, Graph Theory, Third Edition, Springer, 2005.

*[G] A. Georgakopoulos, Oberwolfach reports, 2007.

[M] Bojan Mohar, Problem of the Month

[T] Carsten Thomassen, Reflections on graph theory, J. Graph Theory 10 (1986) 309-324, MathSciNet


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options