 login/create account
login/create account
Cameron, Peter J.
Cores of strongly regular graphs ★★★
Question Does every strongly regular graph have either itself or a complete graph as a core?
Keywords: core; strongly regular
Highly arc transitive two ended digraphs ★★
Author(s): Cameron; Praeger; Wormald
Conjecture If  is a highly arc transitive digraph with two ends, then every tile of
is a highly arc transitive digraph with two ends, then every tile of  is a disjoint union of complete bipartite graphs.
is a disjoint union of complete bipartite graphs.
 is a highly arc transitive digraph with two ends, then every tile of
is a highly arc transitive digraph with two ends, then every tile of  is a disjoint union of complete bipartite graphs.
is a disjoint union of complete bipartite graphs. Keywords: arc transitive; digraph; infinite graph
Universal highly arc transitive digraphs ★★★
Author(s): Cameron; Praeger; Wormald
An alternating walk in a digraph is a walk 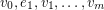 so that the vertex
so that the vertex 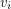 is either the head of both
is either the head of both 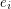 and
and 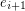 or the tail of both
or the tail of both 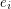 and
and 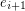 for every
for every 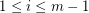 . A digraph is universal if for every pair of edges
. A digraph is universal if for every pair of edges 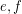 , there is an alternating walk containing both
, there is an alternating walk containing both  and
and 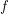
Question Does there exist a locally finite highly arc transitive digraph which is universal?
Keywords: arc transitive; digraph

 Drupal
Drupal CSI of Charles University
CSI of Charles University