 login/create account
login/create account
If  is a graph, we say that a partition of
is a graph, we say that a partition of 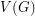 is unfriendly if every vertex has at least as many neighbors in the other classes as in its own.
is unfriendly if every vertex has at least as many neighbors in the other classes as in its own.
It is a simple property that every finite graph  has an unfriendly partition into two sets - just choose a partition of
has an unfriendly partition into two sets - just choose a partition of 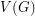 into two sets so that the number of edges with one end in each is maximum. Cowan and Emerson [CE] conjectured that the same property should hold true of infinite graphs. A counterexample to this was constructed by Milner and Shelah [MS], but their construction uses uncountably many vertices, leaving the countable case (highlighted above) still open. In the same article by Milner and Shelah [MS], they show that every graph does have an unfriendly partition into three sets.
into two sets so that the number of edges with one end in each is maximum. Cowan and Emerson [CE] conjectured that the same property should hold true of infinite graphs. A counterexample to this was constructed by Milner and Shelah [MS], but their construction uses uncountably many vertices, leaving the countable case (highlighted above) still open. In the same article by Milner and Shelah [MS], they show that every graph does have an unfriendly partition into three sets.
Curiously, it is quite easy to see that the answer to the above question is yes in the case when all vertices have finite degree, and also in the case when all vertices have infinite degree. The former follows from the unfriendly partition property for finite graphs together with a standard compactness argument. The latter can be achieved with a "back and forth" construction. Thus, the difficult case is the mixed one. Aharoni, Milner, and Prikry [AMP] showed that every graph with only finitely many vertices of infinite degree has an unfriendly partition into two sets, but this seems the extent of our knowledge.
It does not appear that there is any consensus among experts as to whether this conjecture should be true or false.
Bibliography
*[CE] R. Cowan and W. Emerson, Proportional colorings of graphs, unpublished.
[MS] E. C. Milner and S. Shelah, Graphs with no unfriendly partitions. A tribute to Paul Erdös, 373--384, Cambridge Univ. Press, Cambridge, 1990. MathSciNet.
[AMP] R. Aharoni, E. C. Milner, K. Prikry, Unfriendly partitions of a graph. J. Combin. Theory Ser. B 50 (1990), no. 1, 1--10. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University