 login/create account
login/create account
Leader, Imre
Characterizing (aleph_0,aleph_1)-graphs ★★★
Call a graph an 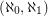 -graph if it has a bipartition
-graph if it has a bipartition 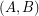 so that every vertex in
so that every vertex in  has degree
has degree 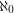 and every vertex in
and every vertex in  has degree
has degree 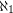 .
.
Problem Characterize the 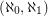 -graphs.
-graphs.
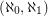 -graphs.
-graphs. Keywords: binary tree; infinite graph; normal spanning tree; set theory
Few subsequence sums in Z_n x Z_n ★★
Conjecture For every 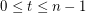 , the sequence in
, the sequence in 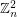 consisting of
consisting of 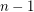 copes of
copes of 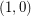 and
and  copies of
copies of 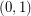 has the fewest number of distinct subsequence sums over all zero-free sequences from
has the fewest number of distinct subsequence sums over all zero-free sequences from 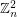 of length
of length 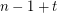 .
.
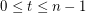 , the sequence in
, the sequence in 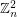 consisting of
consisting of 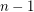 copes of
copes of 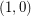 and
and  copies of
copies of 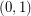 has the fewest number of distinct subsequence sums over all zero-free sequences from
has the fewest number of distinct subsequence sums over all zero-free sequences from 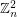 of length
of length 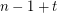 .
. Keywords: subsequence sum; zero sum

 Drupal
Drupal CSI of Charles University
CSI of Charles University