 login/create account
login/create account
Funcoidal products inside an inward reloid
Conjecture (solved) If 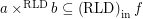 then
then 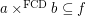 for every funcoid
for every funcoid  and atomic f.o.
and atomic f.o.  and
and  on the source and destination of
on the source and destination of  correspondingly.
correspondingly.
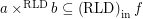 then
then 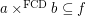 for every funcoid
for every funcoid  and atomic f.o.
and atomic f.o.  and
and  on the source and destination of
on the source and destination of  correspondingly.
correspondingly. A stronger conjecture:
Conjecture If 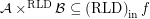 then
then 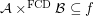 for every funcoid
for every funcoid  and
and 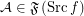 ,
, 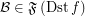 .
.
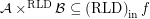 then
then 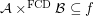 for every funcoid
for every funcoid  and
and 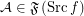 ,
, 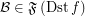 .
. See Algebraic General Topology for definitions of used concepts.
Bibliography
*Victor Porton. Algebraic General Topology
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University