Home » Subject » Geometry » Polytopes

Extension complexity of (convex) polygons

Importance: Medium ✭✭
Author(s):
Subject: Geometry
» Polytopes
Keywords: polytope, projection, extension complexity, convex polygon
Recomm. for undergrads: no
Posted by: DOT
on: August 13th, 2011

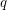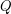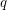The extension complexity of a polytope $ P $ is the minimum number $ q $ for which there exists a polytope $ Q $ with $ q $ facets and an affine mapping $ \pi $ with $ \pi(Q) = P $.

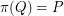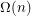Question   Does there exists, for infinitely many integers $ n $, a convex polygon on $ n $ vertices whose extension complexity is $ \Omega(n) $?

The extension complexity of a polytope is bounded from above by its number of vertices. Thus, a convex polygon with $ n $ vertices has extension complexity $ O(n) $.

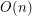Some regular convex polygons have extension complexity 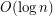$ O(\log n) $ [BTN].

A convex polygon whose points are drawn randomly on a circle has extension complexity 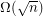$ \Omega(\sqrt n) $ with probability one (follows from [FRT]).

The question asks for the maximal extension complexity of a convex polygon.

A strongly related question is the following.

Question   What is the extension complexity of an $ n $-vertex convex polygon whose vertices are drawn randomly on a circle?

Bibliography

*[BTN] Ben-Tal, A and Nemirovski, A. On polyhedral approximations of the second-order cone. Math. Oper. Res. 26:2 193-205 (2001)

[FRT] Fiorini, S. and Rothvoss, T. and Tiwary, H.R. Extended formulations of polygons. arXiv:1107.0371


* indicates original appearance(s) of problem.
add new comment