 login/create account
login/create account
Recent Activity
Large induced forest in a planar graph. ★★
 verices has an induced forest with at least
verices has an induced forest with at least 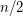 vertices.
vertices. Keywords:
Lovász Path Removal Conjecture ★★
Author(s): Lovasz
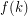 such that if
such that if  is any
is any 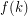 -connected graph and
-connected graph and  and
and 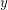 are any two vertices of
are any two vertices of  , then there exists an induced path
, then there exists an induced path  with ends
with ends  and
and 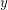 such that
such that 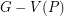 is
is  -connected.
-connected. Keywords:
Partition of a cubic 3-connected graphs into paths of length 2. ★★
Author(s): Kelmans
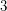 -connected cubic graph on
-connected cubic graph on 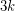 vertices admit a partition into
vertices admit a partition into  paths of length
paths of length 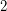 ?
? Keywords:
Decomposing an eulerian graph into cycles with no two consecutives edges on a prescribed eulerian tour. ★★
Author(s): Sabidussi
 be an eulerian graph of minimum degree
be an eulerian graph of minimum degree 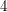 , and let
, and let 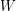 be an eulerian tour of
be an eulerian tour of  . Then
. Then  admits a decomposition into cycles none of which contains two consecutive edges of
admits a decomposition into cycles none of which contains two consecutive edges of 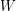 .
. Keywords:
Decomposing an eulerian graph into cycles. ★★
Author(s): Hajós
 vertices can be decomposed into at most
vertices can be decomposed into at most 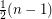 cycles.
cycles. Keywords:
Decomposing a connected graph into paths. ★★★
Author(s): Gallai
 vertices can be decomposed into at most
vertices can be decomposed into at most 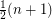 paths.
paths. Keywords:
Melnikov's valency-variety problem ★
Author(s): Melnikov
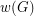 of a graph
of a graph  is the number of different degrees in
is the number of different degrees in  . Is the chromatic number of any graph
. Is the chromatic number of any graph  with at least two vertices greater than
with at least two vertices greater than 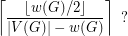
Keywords:
Coloring the union of degenerate graphs ★★
Author(s): Tarsi
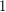 -degenerate graph (a forest) and a
-degenerate graph (a forest) and a 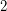 -degenerate graph is
-degenerate graph is  -colourable.
-colourable. Keywords:
Arc-disjoint strongly connected spanning subdigraphs ★★
Author(s): Bang-Jensen; Yeo
 so that every
so that every  -arc-connected digraph contains a pair of arc-disjoint strongly connected spanning subdigraphs?
-arc-connected digraph contains a pair of arc-disjoint strongly connected spanning subdigraphs? Keywords:
Arc-disjoint out-branching and in-branching ★★
Author(s): Thomassen
 such that every
such that every  -arc-strong digraph
-arc-strong digraph  with specified vertices
with specified vertices  and
and  contains an out-branching rooted at
contains an out-branching rooted at  and an in-branching rooted at
and an in-branching rooted at  which are arc-disjoint.
which are arc-disjoint.
Keywords:
Strong edge colouring conjecture ★★
A strong edge-colouring of a graph  is a edge-colouring in which every colour class is an induced matching; that is, any two vertices belonging to distinct edges with the same colour are not adjacent. The strong chromatic index
is a edge-colouring in which every colour class is an induced matching; that is, any two vertices belonging to distinct edges with the same colour are not adjacent. The strong chromatic index 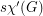 is the minimum number of colours in a strong edge-colouring of
is the minimum number of colours in a strong edge-colouring of  .
.
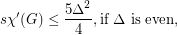
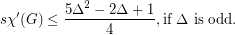
Keywords:
Long directed cycles in diregular digraphs ★★★
Author(s): Jackson
 contains a directed cycle of length at least
contains a directed cycle of length at least 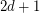 .
. Keywords:
Splitting a digraph with minimum outdegree constraints ★★★
Author(s): Alon
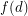 such that the vertices of any digraph with minimum outdegree
such that the vertices of any digraph with minimum outdegree  can be partitioned into two classes so that the minimum outdegree of the subgraph induced by each class is at least
can be partitioned into two classes so that the minimum outdegree of the subgraph induced by each class is at least  ?
? Keywords:
Stable set meeting all longest directed paths. ★★
Author(s): Laborde; Payan; Xuong N.H.
Keywords:
Ádám's Conjecture ★★★
Author(s): Ádám
Keywords:
Caccetta-Häggkvist Conjecture ★★★★
Author(s): Caccetta; Häggkvist
 with minimum outdegree at least
with minimum outdegree at least  has a cycle with length at most
has a cycle with length at most 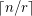
Keywords:
Directed path of length twice the minimum outdegree ★★★
Author(s): Thomassé
 contains a directed path of length
contains a directed path of length 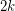 .
. Keywords:
Antidirected trees in digraphs ★★
Author(s): Addario-Berry; Havet; Linhares Sales; Reed; Thomassé
An antidirected tree is an orientation of a tree in which every vertex has either indegree 0 or outdergree 0.
 be a digraph. If
be a digraph. If  , then
, then  contains every antidirected tree of order
contains every antidirected tree of order  .
. Keywords:
Decomposing an even tournament in directed paths. ★★★
Author(s): Alspach; Mason; Pullman
 on an even number of vertices can be decomposed into
on an even number of vertices can be decomposed into 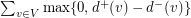 directed paths.
directed paths. Keywords:
Oriented trees in n-chromatic digraphs ★★★
Author(s): Burr
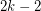 contains every oriented tree of order
contains every oriented tree of order  as a subdigraph.
as a subdigraph. Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University