 login/create account
login/create account
Recent Activity
Monochromatic vertex colorings inherited from Perfect Matchings ★★★
Author(s):
 and
and  are there bi-colored graphs on
are there bi-colored graphs on  vertices and
vertices and  different colors with the property that all the
different colors with the property that all the  monochromatic colorings have unit weight, and every other coloring cancels out?
monochromatic colorings have unit weight, and every other coloring cancels out? Keywords:
Cycle Double Covers Containing Predefined 2-Regular Subgraphs ★★★
Author(s): Arthur; Hoffmann-Ostenhof
 be a
be a  -connected cubic graph and let
-connected cubic graph and let  be a
be a  -regular subgraph such that
-regular subgraph such that 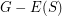 is connected. Then
is connected. Then  has a cycle double cover which contains
has a cycle double cover which contains  (i.e all cycles of
(i.e all cycles of  ).
). Keywords:
Monochromatic reachability in arc-colored digraphs ★★★
Author(s): Sands; Sauer; Woodrow
 , there exists an integer
, there exists an integer 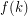 such that if
such that if  is a digraph whose arcs are colored with
is a digraph whose arcs are colored with  colors, then
colors, then  has a
has a  set which is the union of
set which is the union of 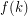 stables sets so that every vertex has a monochromatic path to some vertex in
stables sets so that every vertex has a monochromatic path to some vertex in  .
. Keywords:
3-Decomposition Conjecture ★★★
Author(s): Arthur; Hoffmann-Ostenhof
 has a decomposition into a spanning tree, a family of cycles and a matching.
has a decomposition into a spanning tree, a family of cycles and a matching. Keywords: cubic graph
Which outer reloids are equal to inner ones ★★
Author(s): Porton
Warning: This formulation is vague (not exact).
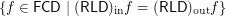 . In other words, simplify this formula.
. In other words, simplify this formula. The problem seems rather difficult.
Keywords:
A diagram about funcoids and reloids ★★
Author(s): Porton
Define for posets with order  :
:
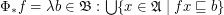 ;
;
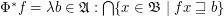 .
.
Note that the above is a generalization of monotone Galois connections (with  and
and  replaced with suprema and infima).
replaced with suprema and infima).
Then we have the following diagram:
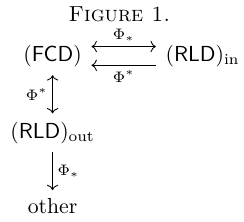
What is at the node "other" in the diagram is unknown.
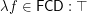 .
. 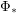 and
and 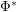 to "other" leads to? Particularly, does repeated applying
to "other" leads to? Particularly, does repeated applying 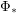 and/or
and/or 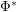 to the node "other" lead to finite or infinite sets?
to the node "other" lead to finite or infinite sets? Keywords: Galois connections
Outward reloid of composition vs composition of outward reloids ★★
Author(s): Porton
 and
and 
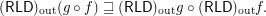
Keywords: outward reloid
Sum of prime and semiprime conjecture ★★
Author(s): Geoffrey Marnell
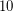 can be represented as the sum of an odd prime number and an odd semiprime .
can be represented as the sum of an odd prime number and an odd semiprime . A funcoid related to directed topological spaces ★★
Author(s): Porton
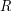 be the complete funcoid corresponding to the usual topology on extended real line
be the complete funcoid corresponding to the usual topology on extended real line ![$ [-\infty,+\infty] = \mathbb{R}\cup\{-\infty,+\infty\} $](/files/tex/3252019c60a83f00ff396d823dbff8040639f409.png) . Let
. Let 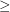 be the order on this set. Then
be the order on this set. Then 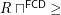 is a complete funcoid.
is a complete funcoid. 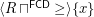 is the infinitely small right neighborhood filter of point
is the infinitely small right neighborhood filter of point ![$ x\in[-\infty,+\infty] $](/files/tex/4e57a21194d8d5a659e259a111ed13a9c23b52a1.png) .
. If proved true, the conjecture then can be generalized to a wider class of posets.
Keywords:
Infinite distributivity of meet over join for a principal funcoid ★★
Author(s): Porton
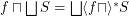 for principal funcoid
for principal funcoid  and a set
and a set  of funcoids of appropriate sources and destinations.
of funcoids of appropriate sources and destinations. Keywords: distributivity; principal funcoid
Weak saturation of the cube in the clique ★
Determine 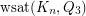 .
.
Keywords: bootstrap percolation; hypercube; Weak saturation
Convex Equipartitions with Extreme Perimeter ★★
Author(s): Nandakumar
To divide a given 2D convex region C into a specified number n of convex pieces all of equal area (perimeters could be different) such that the total perimeter of pieces is (1) maximized (2) minimized.
Remark: It appears maximizing the total perimeter is the easier problem.
Keywords: convex equipartition
Turán Problem for $10$-Cycles in the Hypercube ★★
Author(s): Erdos
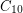 in the hypercube.
in the hypercube. Keywords: cycles; extremal combinatorics; hypercube
Extremal $4$-Neighbour Bootstrap Percolation in the Hypercube ★★
 -neighbour bootstrap process in the hypercube.
-neighbour bootstrap process in the hypercube. Keywords: bootstrap percolation; extremal combinatorics; hypercube; percolation
Saturation in the Hypercube ★★
Author(s): Morrison; Noel; Scott
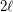 in the
in the  -dimensional hypercube?
-dimensional hypercube? Keywords: cycles; hypercube; minimum saturation; saturation
Cycles in Graphs of Large Chromatic Number ★★
Author(s): Brewster; McGuinness; Moore; Noel
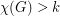 , then
, then  contains at least
contains at least 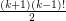 cycles of length
cycles of length 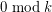 .
. Keywords: chromatic number; cycles
The Double Cap Conjecture ★★
Author(s): Kalai
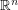 containing no pair of orthogonal vectors is attained by two open caps of geodesic radius
containing no pair of orthogonal vectors is attained by two open caps of geodesic radius 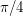 around the north and south poles.
around the north and south poles. Keywords: combinatorial geometry; independent set; orthogonality; projective plane; sphere
Circular flow numbers of $r$-graphs ★★
Author(s): Steffen
A nowhere-zero  -flow
-flow 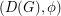 on
on  is an orientation
is an orientation  of
of  together with a function
together with a function 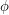 from the edge set of
from the edge set of  into the real numbers such that
into the real numbers such that 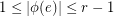 , for all
, for all  , and
, and 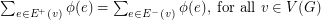 .
.
A 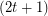 -regular graph
-regular graph  is a
is a 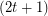 -graph if
-graph if 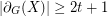 for every
for every 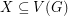 with
with 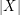 odd.
odd.
 be an integer. If
be an integer. If  is a
is a 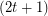 -graph, then
-graph, then 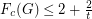 .
. Keywords: flow conjectures; nowhere-zero flows
Circular flow number of regular class 1 graphs ★★
Author(s): Steffen
A nowhere-zero  -flow
-flow 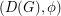 on
on  is an orientation
is an orientation  of
of  together with a function
together with a function 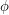 from the edge set of
from the edge set of  into the real numbers such that
into the real numbers such that 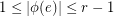 , for all
, for all  , and
, and 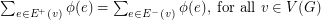 . The circular flow number of
. The circular flow number of  is inf
is inf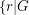 has a nowhere-zero
has a nowhere-zero  -flow
-flow 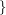 , and it is denoted by
, and it is denoted by 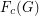 .
.
A graph with maximum vertex degree  is a class 1 graph if its edge chromatic number is
is a class 1 graph if its edge chromatic number is  .
.
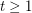 be an integer and
be an integer and  a
a 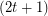 -regular graph. If
-regular graph. If  is a class 1 graph, then
is a class 1 graph, then 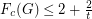 .
. Chromatic number of associahedron ★★
Author(s): Fabila-Monroy; Flores-Penaloza; Huemer; Hurtado; Urrutia; Wood

 Drupal
Drupal CSI of Charles University
CSI of Charles University