 login/create account
login/create account
Woodrow, Robert E.
Monochromatic reachability in arc-colored digraphs ★★★
Author(s): Sands; Sauer; Woodrow
Conjecture For every  , there exists an integer
, there exists an integer 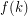 such that if
such that if  is a digraph whose arcs are colored with
is a digraph whose arcs are colored with  colors, then
colors, then  has a
has a 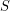 set which is the union of
set which is the union of 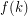 stables sets so that every vertex has a monochromatic path to some vertex in
stables sets so that every vertex has a monochromatic path to some vertex in 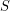 .
.
 , there exists an integer
, there exists an integer 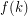 such that if
such that if  is a digraph whose arcs are colored with
is a digraph whose arcs are colored with  colors, then
colors, then  has a
has a 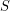 set which is the union of
set which is the union of 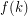 stables sets so that every vertex has a monochromatic path to some vertex in
stables sets so that every vertex has a monochromatic path to some vertex in 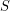 .
. Keywords:
Monochromatic reachability or rainbow triangles ★★★
Author(s): Sands; Sauer; Woodrow
In an edge-colored digraph, we say that a subgraph is rainbow if all its edges have distinct colors, and monochromatic if all its edges have the same color.
Problem Let  be a tournament with edges colored from a set of three colors. Is it true that
be a tournament with edges colored from a set of three colors. Is it true that  must have either a rainbow directed cycle of length three or a vertex
must have either a rainbow directed cycle of length three or a vertex  so that every other vertex can be reached from
so that every other vertex can be reached from  by a monochromatic (directed) path?
by a monochromatic (directed) path?
 be a tournament with edges colored from a set of three colors. Is it true that
be a tournament with edges colored from a set of three colors. Is it true that  must have either a rainbow directed cycle of length three or a vertex
must have either a rainbow directed cycle of length three or a vertex  so that every other vertex can be reached from
so that every other vertex can be reached from  by a monochromatic (directed) path?
by a monochromatic (directed) path? Keywords: digraph; edge-coloring; tournament

 Drupal
Drupal CSI of Charles University
CSI of Charles University